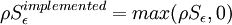Yap correction
From CFD-Wiki
The Yap correction [Yap. C. J. (1987)] consists of a modification of the epsilon equation in the form of an extra source term,  , added to the right hand side of the epsilon equation. The source term can be written as:
, added to the right hand side of the epsilon equation. The source term can be written as:
Where
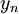 is the normal distance to the nearest wall.
is the normal distance to the nearest wall.
This source term should be added to the epsilon equation in the following way:
Where the epsilon equation has been written in the same way as is in the CFD-Wiki article on low-Re k-epsilon models.
The Yap correction is active in nonequilibrium flows and tends to reduce the departure of the turbulence length scale from its local equilibrium level. It is an ad-hoc fix which seldom causes any problems and often improves the predictions.
Yap showed strongly improved results with the k-epsilon model in separated flows when using this extra source term. The Yap correction has also been shown to improve results in a stagnation region. Launder [Launder, B. E. (1993)] recommends that the Yap correction should always be used with the epsilon equation.
Implementation issues
The Yap source term contains the explicit distance to the nearest wall,  . This distance is sometimes difficult to efficiently calculate in complex geometries. In structured grids, the coordinate distance to the nearest wall can be used as an approximation. Otherwise, a brute force calculation must be used which greatly benefits from a multi grid approach. In topologies with domain boundaries that are not walls the problem becomes more complex, because the non-wall boundaries will block the direct path to the wall boundaries. A simple loop over length must now be accompanied by topological path checking. This makes the Yap correction most suitable for use in a structured code where some normal wall distance is readily available. There are several alternative formulations that can be used instead though (anyone have the references??).
. This distance is sometimes difficult to efficiently calculate in complex geometries. In structured grids, the coordinate distance to the nearest wall can be used as an approximation. Otherwise, a brute force calculation must be used which greatly benefits from a multi grid approach. In topologies with domain boundaries that are not walls the problem becomes more complex, because the non-wall boundaries will block the direct path to the wall boundaries. A simple loop over length must now be accompanied by topological path checking. This makes the Yap correction most suitable for use in a structured code where some normal wall distance is readily available. There are several alternative formulations that can be used instead though (anyone have the references??).
When implementing the Yap correction it is common to use it only if the source term is positive. Hence:
References
Launder, B. E. (1993), "Modelling Convective Heat Transfer in Complex Turbulent Flows", Engineering Turbulence Modeling and Experiments 2, Proceedings of the Second International Symposium, Florence, Italy, 31 May - 2 June 1993, Edited by W. Rodi and F. Martelli, Elsevier, 1993, ISBN 0444898026.
Yap, C. J. (1987), Turbulent Heat and Momentum Transfer in Recirculating and Impinging Flows, PhD Thesis, Faculty of Technology, University of Manchester, United Kingdom.

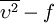 model
model
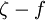 model
model
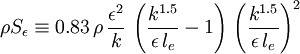
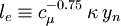
![\frac{\partial}{\partial t} \left( \rho \epsilon \right) +
\frac{\partial}{\partial x_j}
\left[
\rho \epsilon u_j - \left( \mu + \frac{\mu_t}{\sigma_\epsilon} \right)
\frac{\partial \epsilon}{\partial x_j}
\right]
=
\left( C_{\epsilon_1} f_1 P - C_{\epsilon_2} f_2 \rho \epsilon \right)
\frac{\epsilon}{k}
+ \rho E
+ \rho S_\epsilon](/W/images/math/a/7/5/a758d253c1fa5a752e369768c8bacac5.png)