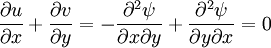Stream function
From CFD-Wiki
The stream function is a scalar field variable which is constant on each streamline. It exists only in two-dimensional and axisymmetric flows.
On a streamline in two-dimensional flow
The equation of a streamline in two-dimensions is
Comparing the two equations, we have
Conversely, the stream function at any point 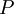 can be obtained from the velocity field by a line integral
can be obtained from the velocity field by a line integral
where 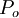 is some reference point and one can assume
is some reference point and one can assume 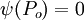 since the stream function is determined only upto a constant.
since the stream function is determined only upto a constant.
If the flow is incompressible, then the continuity equation is identically satisfied

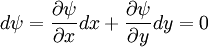

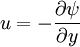
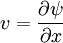
![\psi(P) = \psi(P_o) + \int_{P_o}^P [ v(x,y,t) dx - u(x,y,t) dy ]](/W/images/math/0/6/1/061c8e98a4c2cb20abf21f9183e0332e.png)