PISO algorithm - Pressure Implicit with Split Operator
From CFD-Wiki
Contents |
Introduction
PISO algorithm (Pressure implicit with splitting of operator) was proposed by Issa in 1986 without iterations and with large time steps and a lesser computing effort. It is an extension of the SIMPLE algorithm used in CFD (computational fluid dynamics) to solve the Navier-Stokes equations. PISO is a pressure-velocity calculation procedure for the Navier-Stokes equations developed originally for non-iterative computation of unsteady compressible flow, but it has been adapted successfully to steady-state problems.
PISO involves one predictor step and two corrector steps and is designed to satisfy mass conservation using predictor-corrector steps.
Algorithm Steps
The algorithm can be summed up as follows:
- Set the boundary conditions.
- Solve the discretized momentum equation to compute an intermediate velocity field.
- Compute the mass fluxes at the cells faces.
- Solve the pressure equation.
- Correct the mass fluxes at the cell faces.
- Correct the velocities on the basis of the new pressure field.
- Update the boundary conditions.
- Repeat from 3 for the prescribed number of times.
- Increase the time step and repeat from 1.
As already seen for the SIMPLE algorithm, the steps 4 and 5 can be repeated for a prescribed number of time to correct for non-orthogonality.
predictor step
guess the pressure field 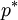 and get velocity field component
and get velocity field component 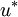 and
and 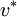 using Discretized momentum equation.The initial guess for the pressure may be correct or not.
using Discretized momentum equation.The initial guess for the pressure may be correct or not.
corrector step 1
velocity component obtain from predictor step may not satisfy the continuity equation ,so we define correction factor p',v',u' pressure field and velocity field. solve momentum equation by put correct pressure 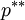 field and get corresponding correct velocity component
field and get corresponding correct velocity component 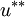 and
and 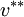 .
.
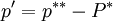
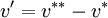
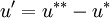
where ;
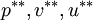 :correct pressure field and velocity component
:correct pressure field and velocity component
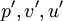 :correction in pressure field and correction in velocity component
:correction in pressure field and correction in velocity component
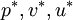 :guessed pressure field and velocity component
:guessed pressure field and velocity component
we define as above 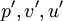 .
by put correct term of pressure field
.
by put correct term of pressure field 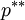 in discretized momentum equation we get correct velocity component
in discretized momentum equation we get correct velocity component 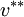 and
and 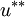 . Once the pressure correction
. Once the pressure correction 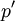 is known we can find correction component for the velocity
is known we can find correction component for the velocity 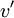 and
and 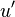 .
.
corrector step2
in piso another corrector step .
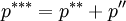 ;
; 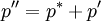
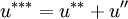 ;
; 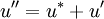
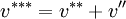 ;
; 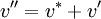
where :
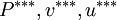 are respectively correct pressure field and correct velocity component
are respectively correct pressure field and correct velocity component
and 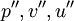 are second correction pressure and velocity field.
are second correction pressure and velocity field.
set 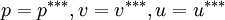 where ;
where ; 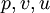 are correct pressure and velocity field
are correct pressure and velocity field
Advantages and disadvantages
- Generally gives more stable results and takes less CPU time but not suitable for all processes.
- Suitable numerical schemes for solving the pressure-velocity linked equation.
- For laminar backward facing step PISO is faster than SIMPLE but it slower for concerning flow through heated fin.
- If momentum and scalar equation have weak or no coupling then PISO is better than SIMPLEC.
References
1. Solution of the implicitly discretized fluid flow equations by operator-splitting, Journal of Computational Physics 62 by R. Issa
2.An Introduction to Computational Fluid Dynamics The Finite Volume Method, 2/e
By Versteeg ISBN 978-0131274983
3.Computational Fluid Dynamics for Engineers By Bengt Andersson
Ronnie Andersson
Love Håkansson
Mikael Mortensen
Rahman Sudiyo
Berend van Wachem
ISBN 978-1-107-01895-2
4.Computational Fluid Dynamics in Fire Engineering: Theory, Modelling and Practice
By Guan Heng Yeoh, Kwok Kit Yuen ISBN 978-0750685894
5.http://openfoamwiki.net/index.php/OpenFOAM_guide/The_PISO_algorithm_in_OpenFOAM
6.Computational fluid dynamics BY T. J. CHUNG University of Alabama in Huntsville ISBN 0 521 59416 2
7.Computational method for fluid dynamics by Joel H.Ferziger,Milovan Peric ISBN 3-540-42074-6
