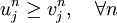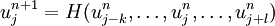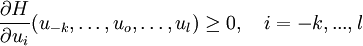Monotone scheme

From CFD-Wiki

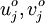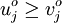A scheme is said to be monotone if for two initial conditions $u^o_j, v^o_j$ with $u^o_j \ge v^o_j$ , then

$u^n_j \ge v^n_j, \quad \forall n$

A monotone scheme for a scalar conservation law can be shown to converge to the unique entropy satisfying solution. However, monotone schemes can be at most first order accurate.

If the scheme can be written as

$u^{n+1}_j = H(u^n_{j-k}, \ldots, u^n_j, \ldots, u^n_{j+l})$

then it is monotone if and only if it is an increasing function of all its arguments. If 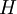$H$ is a differentiable function of its arguments, then the scheme is monotone if

$\frac{\partial H}{\partial u_i}(u_{-k}, \dots, u_{o}, \ldots, u_{l}) \ge 0, \quad i=-k,...,l$

We have the following relationship between monotone, TVD and monotonicity preserving schemes,

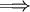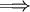Monotone scheme $\Longrightarrow$ TVD scheme $\Longrightarrow$ Monotonicity preserving scheme

Monotone scheme

From CFD-Wiki

Views

My wiki

wiki navigation

wiki search

wiki toolbox