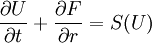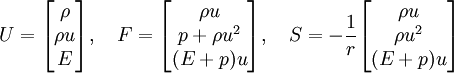Explosion test in 2-D
From CFD-Wiki
The two dimensional Euler equations are solved on a square domain 2x2 in the xy-plane. The initial conditions consists of circular discontinuity of radius 0.4 centered at (1,1). The values inside and outside the circle are given in the table below.
| Variable | Inside | Outside |
| Density | 1.0 | 0.125 |
| x velcity | 0.0 | 0.0 |
| y velocity | 0.0 | 0.0 |
| Pressure | 1.0 | 0.1 |
A typical mesh size that can be used consists of 100x100 cells. It is good to use cell-averaged data as initial conditions. Otherwise the initial data consists of a staircase configuration leading to small amplitude waves at initial times.
The solution exhibits a circular shock wave traveling away from the center, a circular contact surface traveling in the same direction and a circular rarefaction traveling towards the origin (1,1). As time evolves, a complex wave pattern emerges. The circular shock wave travels outwards and becomes weaker. The contact surface follows the shock and also becomes weaker; at some point in time the contact comes to rest and then travels inwards. The rarefaction traveling towards the center reflects, as a rarefaction, and over-expands the flow so as to create an inward traveling shock wave; this circular shock wave implodes into the origin, reflects and travels outwards colliding with the contact surface.
Since the solution has circular symmetry, the 2-D Euler equations can be reduced to 1-D Euler equations in the radial coordinate r,
where
This 1-D problem can be solved using a large number of grid points. The 1-D solution can then be used to assess the accuracy of the 2-D solution.