Basic aspects of discretization
From CFD-Wiki
There are various methods of discretization, which can broadly be classified into mesh (grid) methods and mesh-free methods. Currently (as of 2014), mainly mesh methods are being used.
Contents |
Mesh Methods
These methods involve two steps:
- Meshing - divide the region ("domain") into smaller regions. These smaller regions may be triangles and rectangles (in 2D) and tetrahedrons, hexahedrons (in 3D) and other types of geometric entities. The vertices of these geometric entities are called nodes.
- Discretization of the governing equations over the mesh
Finite Differences
The general idea behind discretization is to break a domain into a mesh, and then replace derivatives in the governing equation with difference quotients. There are several ways in which this can be done - the most prominent being forward difference, backward difference and central difference.
To give an example, in the forward difference scheme, derivatives are approximated as follows.
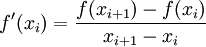 where subscripts are node indices of the mesh.
where subscripts are node indices of the mesh.
The article on finite difference method is here.
Finite Volumes
The article on finite volume method is here.
Finite Elements
Meshfree Methods
Several kinds of meshfree methods are also in use. Many are being actively developed. Some such methods are:
- Smooth Particle Hydrodynamics (SPH)
- Finite Pointset Method (FPM)
