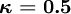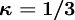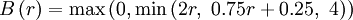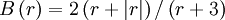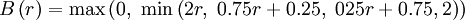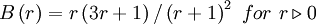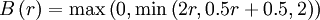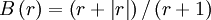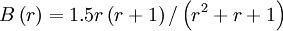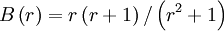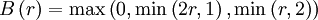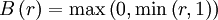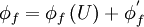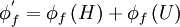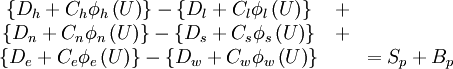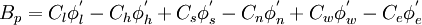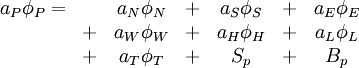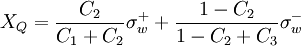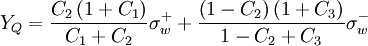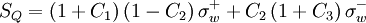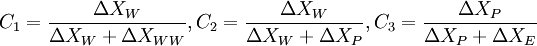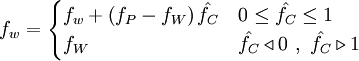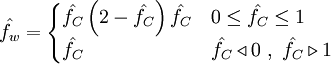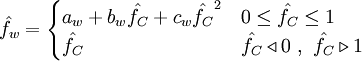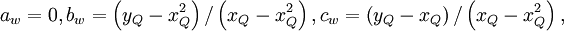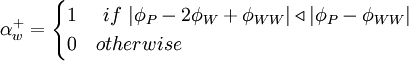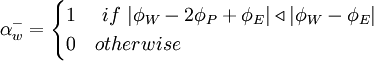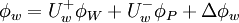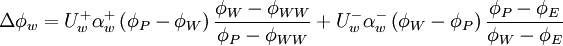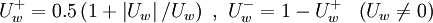Approximation Schemes for convective term
From CFD-Wiki
When we shall fill this page, I offer to make common identifications, because in different issues was used different notation.
Also I beg everybody to help me with original works. Later I shall write, what is necessary. If anyone have literature connected with convective schemes, please drop me a line.
Michail
Discretisation Schemes for convective terms in General Transport Equation. Finite-Volume Formulation, structured grids
Introduction
Here is described the discretization schemes of the convective terms in the finite-volume equations. The accuracy, numerical stability and the boundness of the solution depends on the numerical scheme used for these terms. The central issue is the specification of an appropriate relationship between the convected variable, stored at the cell centre and its value at each of the cell faces.
Basic Equations of CFD
All the conservation equations can be written in the same generic differential form:
|
| (1) |
Equation (1) is integrated over a control volume and the following discretised equation for 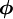 is produced:
is produced:
|
| (2) |
where 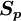 is the source term for the control volume
is the source term for the control volume 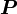 , and
, and 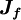 and
and 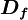 represent, respectively, the convective and diffusive fluxes of
represent, respectively, the convective and diffusive fluxes of 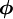 across the control-volume face
across the control-volume face 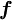
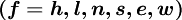
The convective fluxes through the cell faces are calculated as:
|
| (1) |
where 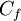 is the mass flow rate across the cell face
is the mass flow rate across the cell face 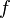 . The convected variable
. The convected variable 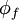 associated with this mass flow rate is usually stored at the cell centres, and thus some form of interpolation assumption must be made in order to determine its value at each cell face. The interpolation procedure employed for this operation is the subject of the various schemes proposed in the literature and the accuracy, stability and boundedness of the solution depends on the procedure used.
associated with this mass flow rate is usually stored at the cell centres, and thus some form of interpolation assumption must be made in order to determine its value at each cell face. The interpolation procedure employed for this operation is the subject of the various schemes proposed in the literature and the accuracy, stability and boundedness of the solution depends on the procedure used.
In general, the value of 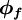 can be explicity formulated in terms of its neighbouring nodal values by a functional relationship of the form:
can be explicity formulated in terms of its neighbouring nodal values by a functional relationship of the form:
|
| (1) |
where 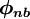 denotes the neighbouring-node
denotes the neighbouring-node 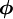 values.
Combining equations (\ref{eq3}) through (\ref{eq4a}), the discretised equation becomes:
values.
Combining equations (\ref{eq3}) through (\ref{eq4a}), the discretised equation becomes:
|
| (1) |
Convection Schemes
All the convection schemes involve a stencil of cells in which the values of 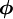 will be used to construct the face value
will be used to construct the face value 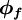
Where flow is from left to right, and 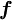 is the face in question.
is the face in question.
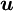 - mean Upstream node
- mean Upstream node
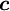 - mean Central node
- mean Central node
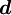 - mean Downstream node
- mean Downstream node
Basic Discretisation schemes
Central Differencing Scheme (CDS)
The most natural assumption for the cell-face value of the convected variable 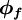 would appear to be the CDS, which calculates the cell-face value from:
would appear to be the CDS, which calculates the cell-face value from:
|
| (1) |
This scheme is 2nd-order accurate, but is unbounded so that unphysical oscillations appear in regions of strong convection and also in the presence of discontinuities such as shocks. The CDS may be used directly in very low Reynolds-number flows where diffusive effects dominate over convection.
Upwind Differencing Scheme (UDS)
The UDS assumes that the convected variable at the cell fase 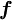 is the same as the upwind cell-centre value:
is the same as the upwind cell-centre value:
|
| (1) |
The UDS is unconditionally bounded and highly stable, but as noted earlier it is only 1st-order accurate in terms of truncation error and may produce severe numerical diffusion. The scheme is therefore highly diffusive when the flow direction is skewed relative to the grid lines.
Hybrid Differencing Scheme (HDS also HYBRID)
The HDS of Spalding [1972] switches the discretisation of the convection terms between CDS and UDS according to the local cell Peclet number as follows:
|
| (1) |
|
| (1) |
The cell Peclet number is defined as:
|
| (1) |
in which 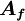 and
and 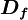 are respectively, the cell-face area and physical diffusion coefficient. When
are respectively, the cell-face area and physical diffusion coefficient. When 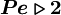 ,CDS calculations tends to become unstable so that theHDS reverts to the UDS. Physical diffusion is ignored when
,CDS calculations tends to become unstable so that theHDS reverts to the UDS. Physical diffusion is ignored when 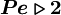 .
.
The HDS scheme is marginally more accurate than the UDS, because the 2nd-order CDS will be used in regions of low Peclet number.
Power-Law Scheme
- Patankar, S. V. (1980), Numerical Heat Transfer and Fluid Flow, ISBN 0070487405, McGraw-Hill, New York.
High Resolution Schemes (HRS)
Classification of High Resolution Schemes
HRS can be classified as linear or non-linear, where linear means their coefficients are not direct functions of the convected variable when applied to a linear convection equation. It is important to recognise that linear convection schemes of 2nd-order accuracy or higher may suffer from unboudedness, and are not unconditionally stable.
Non-linear schemes analyse the solution within the stencil and adapt the discretisation to avoid any unwanted behavior, such as unboundedness (see Waterson [1994]). These two types of schemes may be presented in a unified way by use of the Flux-Limiter formulation (Waterson and Deconinck [1995]), which calculates the cell-face value of the convected variable from:
|
| (1) |
where 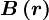 is termed a limiter function and the gradient ration
is termed a limiter function and the gradient ration 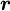 is defined as:
is defined as:
|
| (1) |
The generalisation of this approach to handle non-uniform meshes has been given by Waterson [1994]
From equation (\ref{eq9}) it can be seen that 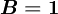 gives the UDS and
gives the UDS and 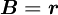 gives the CDS.
gives the CDS.
Please note that linear does not mean first order
Linear schemes
Linear schemes are those for which 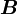 is linear function of
is linear function of 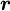
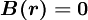 is upwind differencing (first-order accurate)
is upwind differencing (first-order accurate)
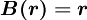 is central differencing (second-order accurate)
is central differencing (second-order accurate)
Kappa Schemes and Other schemes
Higher order schemes are usually members of the 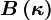 class, for which
class, for which
|
| (1) |
Using this equation face variable can be expressed:
in usual variabales
|
| (1) |
in normalised variables
|
| (1) |
The main schemes are
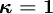
CDS (central differencing scheme) 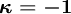
QUICK (quadaratic upwind scheme) LUS (linear upwind scheme) Fromm CUS (cubic upwind scheme)
Non-Linear schemes
Non-linear schemes are those for which 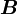 is not a linear function of
is not a linear function of 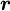 . They fall into three categories, depending on the linear schemes on which they are based.
. They fall into three categories, depending on the linear schemes on which they are based.
-
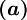 QUICK based:
QUICK based:
SMART (piecewise linear, bounded)
|
| (1) |
H-QUICK (smooth)
|
| (1) |
UMIST (piecewise linear , bounded)
|
| (1) |
CHARM (smooth, bounded)
|
| (1) |
|
| (1) |
-
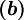 Fromm based:
Fromm based:
MUSCL (piecewise linear)
|
| (1) |
van Leer (smooth)
|
| (1) |
OSPRE (smooth)
|
| (1) |
van Albada (smooth)
|
| (1) |
-
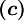 other:
other:
Superbee (piecewise linear)
|
| (1) |
Minmod (piecewise linear)
|
| (1) |
- Waterson, N. P and Deconinck, H (1995), "A unified approach to the desing and application of bounded high-order covection schemes", VKI preprint 1995-21.
- Waterson, N. P. (1994), "Development of bounded high-order convection scheme for general industrial applications", VKI Project Report 1994-33.
Numerical Implementation of HRS
The HRS schemes can be introduced into equation (\ref{eq4b}) by using the deffered correction procedure of Rubin and Khosla [1982]. This procedure express the cell-face value 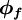 by:
by:
|
| (1) |
where 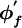 is a higher-order correction which represents the difference between the UDS face value
is a higher-order correction which represents the difference between the UDS face value 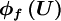 and the higher-order scheme value
and the higher-order scheme value 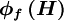 , i.e.
, i.e.
|
| (1) |
If equation (\ref{eq10a}) is substituted into equation (\ref{eq4b}), the resulting discretised equation is:
|
| (1) |
where 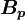 is the deferred-correction source terms, given by:
is the deferred-correction source terms, given by:
|
| (1) |
This treatment leads to a diagonally dominant coefficient matrix since it is formed using the UDS.
The final form of the discretised equation:
|
| (1) |
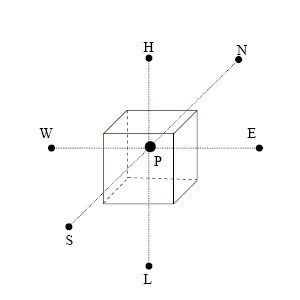
Subscrit 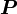 represents the current computational cell;
represents the current computational cell; 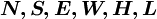 represent the six neighbouring cells and
represent the six neighbouring cells and 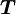 represents the previous timestep (transistent cases only)
represents the previous timestep (transistent cases only)
The coefficients contain the appropriate contributions from the transient, convective and diffusive terms in (\ref{eq1})
P.K. Khosla and S.G. Rubin (1974), "A diagonally dominant second order accurate implicit scheme", Comput. Fluids, 2 207-209.
S.G.Rubin and P.K.Khoshla (1982), "Polynomial interpolation method for viscous flow calculations", J. Comp. Phys., Vol. 27, pp. 153.
Normalised Variables Formulation (NVF)
B.P.Leonard (1988), "Simple high-accuracy resolution program for convective modelling of discontinuities", International J. Numerical Methods Fluids, 8:1291-1318.
Normalised Variable and Space Formulation (NVSF)
Darwish M.S. and Moukalled F. (1994), "Normalized Variable and Space Formulation Methodology for High-Resolution Schemes", Num. Heat Trans., part B, vol. 26, pp. 79-96.
Alves M.A., Cruz P. Mendes A. Magahaes F.D. Pinho F.T., Oliveira P.J. (2002), "Adaptive multiresolution approach for solution of hyperbolic PDEs", Computational Methods in Applied Mechanics and Engineering, 191, 3909-3928.
Normalised Variables Diagram (NVD)
According to Leonard [1988], for any (in general nonlinear) characteristics in the normalized variable diagram (see figure below):
- Passing through
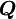 is necessary and sufficient for second-order accuracy
is necessary and sufficient for second-order accuracy
- Passing through
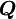 with a slope of 0.75 (for a uniform grid) is necessary and sufficient for third-order accuracy
with a slope of 0.75 (for a uniform grid) is necessary and sufficient for third-order accuracy
The horizontal and vertical coordinates of point 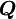 in the normalized variable diagram and the slope of the characteristics at the point
in the normalized variable diagram and the slope of the characteristics at the point 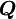 for preserving the third-order accuracy for a nonuniform grid can be obtained by simple algebra using eqs. [.....]
for preserving the third-order accuracy for a nonuniform grid can be obtained by simple algebra using eqs. [.....]
|
| (1) |
|
| (1) |
|
| (1) |
where
|
| (1) |
For a uniform qrid, 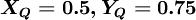 and
and 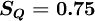
Normalised variable diagram for various well-known schemes
Total Variation Diminishing (TVD)
A. Harten (1984), "On a class of high resolution total-variation stable finite difference schemes", SIAM J. Num. Analysis, 21, p1.
P. K. Sweby (1984), "High resolution schemes using flux-limiters for hyperbolic conservation laws", SIAM J. Num. Analysis, 21, p995.
S. Godunov theorem
Total Variation Diminishing Diagram (Sweby diagram)
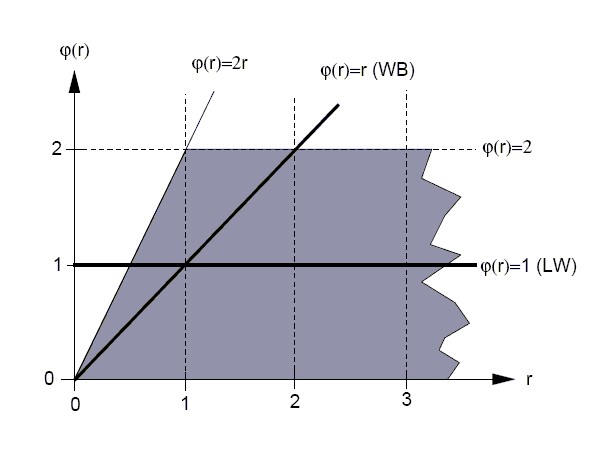
Convection Boundedness Criterion (CBC)
Choi S.K., Nam H.Y. and Cho M. (1995), "A comparison of high-order bounded convection schemes", Computational Methods in Applied Mechanics and engineering, Vol. 121, pp. 281-301.
Gaskell P.H. and Lau A.K.C. (1988), "Curvative-compensated convective transport: SMART, a new boundedness-preserving trasport algorithm", International Journal for Numerical Methods in Fluids, Vol. 8, No. 6, pp. 617-641.
Gaskel and Lau have formulated the CBC as follows. A numerical approximation to 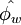 is bounded if:
is bounded if:
- for
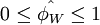 ,
, 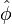 is bounded below by the function
is bounded below by the function 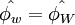 and above by unity and passes through the points (0,0) and (1,1)
and above by unity and passes through the points (0,0) and (1,1)
- for
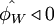 or
or 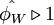 ,
, 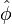 is equal to
is equal to 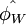
The CBC is clearly illustrated in figure below, where the line 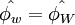 and the shaded area are the region over which the CBC is valid. The importance of the CBC is to provide a sufficient and necessary condition for guaranteeing the bounded solution if at most three neighbouring nodal values are used to approximate face values. It is well known that the positivity of finite-difference coefficients is also a sufficient condition for boundedness, but this is overly stringent, for the existense of negative coefficients does not neccesarily lead to over- or undershoots.
and the shaded area are the region over which the CBC is valid. The importance of the CBC is to provide a sufficient and necessary condition for guaranteeing the bounded solution if at most three neighbouring nodal values are used to approximate face values. It is well known that the positivity of finite-difference coefficients is also a sufficient condition for boundedness, but this is overly stringent, for the existense of negative coefficients does not neccesarily lead to over- or undershoots.
Schemes
Linear
SOU - Second Order Upwind (also LUDS or UDS-2)
S.P.Vanka ({{{year}}}), "Second-order upwind differencing ina recirculating flow", AIAA J., 25, 1435-1441.
R.F.Warming and R.M. Beam
Upwind second order difference schemes and applications in aerodynamics flows
AIAA J. 14 (1976) 1241-1249
Skew - Upwind
G.D.Raithby , Skew upstream differencing schemes for problems involving fluid flow, Computational Methods Applied Mech. Engineering, 9, 153-164 (1976)
QUICK - Quadratic Upwind Interpolation for Convective Kinematics (also UDS-3)
B.P.Leonard, A stable and accurate modelling procedure based on quadratic interpolation, Comput. Methods Appl. Mech. Engrg. 19 (1979) 58-98
LUS - Linear Upwind Scheme
H.C.Price, R.S. Varga and J.E.Warren , Application of oscillation matrices to diffusion-convection equations, Journal Math. and Phys., Vol. 45, p.301, (1966)
Fromm - Fromm's Upwind Scheme
CUDS - Cubic Upwind Difference Scheme (also CUS)
Non-Linear QUICK based
SMART - Sharp and Monotonic Algorithm for Realistic Transport
P.H.Gaskell and A.C.K. Lau, Curvature-compensated convective transport: SMART, a new boundedness preserving transport algorithm, International J. Numer. Methods Fluids 8 (1988) 617-641
SMARTER - SMART Efficiently Revised
J.K. Shin and Y.D. Choi
Study on the improvement of the convective differencing scheme for the high-accuracy and stable resolution of the numerical solution
Trans. KSME 16(6) (1992) 1179-1194 (in Korean)
WACEB
Song B., Liu G.B., Kam K.Y., Amano R.S.
On a higher-order bounded discretization schemes
International Journal for Numerical Methods in Fluids, 2000, 32, 881-897
VONOS - Variable-Order Non-Oscillatory Scheme
Varonos A., Bergeles G., Development and assessment of a Variable-Order Non-oscillatory Scheme for convection term discretization // International Journal for Numerical Methods in Fluids. 1998. 26, N 1. 1-16
CHARM - Cubic / Parabolic High-Accuracy Resolution Method
G.Zhou , Numerical simulations of physical discontinuities in single and multi-fluid flows for arbitrary Mach numbers, PhD Thesis, Chalmers University of Technology, Sweden (1995)
Gang Zhou, Lars Davidson and Erik Olsson
Transonic Inviscid / Turbulent Airfoil Flow Simulations Using a Pressure Based Method with High Order Schemes
Lecture notes in Physics, No. 453, pp. 372-377, Springler-Verlag, Berlin, (1995)
UMIST - Upstream Monotonic Interpolation for Scalar Transport
F.S.Lien and M.A.Leschziner , Upstream Monotonic Interpolation for Scalar Transport with application to complex turbulent flows, International Journal for Numerical Methods in Fluids, Vol. 19, p.257, (1994)
Fromm based
MUSCL - Monotonic Upwind Scheme for Conservation Laws
Lien F.S. and Leschziner M.A. , Proc. 5th Int. IAHR Symp. on Refind Flow Modelling and Turbulence Measurements, Paris, Sept. 1993
van Leer limiter
van Albada
OSPRE
ULTIMATE Universal Limiter
Chakravarthy-Osher limiter
Sweby \Phi - limiter
Superbee
MINMOD - MINimum MODulus
Harten A. High resolution schemes using flux limiters for hyperbolic conservation laws. Journal of Computational Physics 1983; 49: 357-393
A. Harten
High Resolution Schemes for Hyperbolic Conservation Laws
J. Comp. Phys., vol. 49, no. 3, pp. 225-232, 1991
ISNAS - Interpolation Scheme which is Nonoscillatory for Advected Scalars
Third-order flux-limiter scheme
M. Zijlema , On the construction of a third-order accurate monotone convection scheme with application to turbulent flows in general domains. International Journal for numerical methods in fluids, 22:619-641, 1996.
SOUCUP - Second-Order Upwind Central differnce-first order UPwind
Zhu J. (1992), "On the higher-order bounded discretization schemes for finite volume computations of incompressible flows", Computational Methods in Applied Mechanics and Engineering. 98. 345-360.
J. Zhu, W.Rodi (1991), "A low dispersion and bounded convection scheme", Comp. Meth. Appl. Mech.&Engng, Vol. 92, p 225.
COPLA - COmbination of Piecewise Linear Approximation
HLPA - Hybrid Linear / Parabolic Approximation
Zhu J. Low Diffusive and oscillation-free convection scheme // Communications and Applied Numerical Methods. 1991. 7, N3. 225-232.
Zhu J., Rodi W. A low dispersion and bounded discretization schemes for finite volume computations of incompressible flows // Computational Methods for Applied Mechanics and Engineering. 1991. 92. 87-96
In this scheme, the normalized face value is approximated by a combination of linear and parabolic charachteristics passing through the points, O, Q, and P in the NVD. It satisfies TVD condition and is second-order accurate
Usual variables
|
| (2) |
Normalized variables - uniform grids
|
| (2) |
Normalized variables - non-uniform grids
|
| (2) |
where
|
| (2) |
Implementation
Using the switch factors:
for 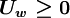
|
| (2) |
for 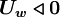
|
| (2) |
and taken all the possible flow directions into account, the un-normalized form of equation can be written as
|
| (2) |
where
|
| (2) |
|
| (2) |
CLAM - Curved-Line Advection Method
Van Leer B. , Towards the ultimate conservative difference scheme. II. Monotonicity and conservation combined in a second-order scheme. Journal of Computational Physics 1974; 14:361-370
SHARP - Simple High Accuracy Resolution Program
B.P.Leonard, Simple high-accuracy resolution rogram for convective modelling of discontinuities, International J. Numerical Methods Fluids 8 (1988) 1291-1381
LPPA - Linear and Piecewise / Parabolic Approximasion
GAMMA
CUBISTA - Convergent and Universally Bounded Interpolation Scheme for the Treatment of Advection
M.A. Alves, P.J.Oliveira, F.T. Pinho, A convergent and Universally Bounded Interpolation Scheme for the Treatment of Advection // International Lournal For Numerical Methods in Fluids 2003, 41; 47-75
Summary of Discretizations Schemes
Discretizations Schemes Estimation of order
Selection advice
Comparison of Discretizations Schemes
Numerical examples
Pure convection of a scalar step by a rotating velocity field (Smith-Hutton test)
R.M.Smith and A.G.Hutton (1982), "The numerical treatment of advection: A performance comparison of current methods", Numerical Heat Transfer, Vol. 5, p439.

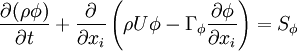
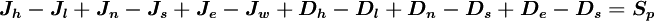
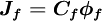
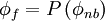
![\left\{ D_{h} + C_{h} \left[ P \left( \phi_{nb} \right) \right]_{h} \right\} -
\left\{ D_{l} + C_{l} \left[ P \left( \phi_{nb} \right) \right]_{l} \right\} +
\left\{ D_{n} + C_{n} \left[ P \left( \phi_{nb} \right) \right]_{n} \right\} -
\left\{ D_{s} + C_{s} \left[ P \left( \phi_{nb} \right) \right]_{s} \right\} +
\left\{ D_{e} + C_{e} \left[ P \left( \phi_{nb} \right) \right]_{e} \right\} -
\left\{ D_{w} + C_{w} \left[ P \left( \phi_{nb} \right) \right]_{w} \right\} = S_{p}](/W/images/math/8/a/7/8a710ce35af1c5c95cf741524ecd18f6.png)

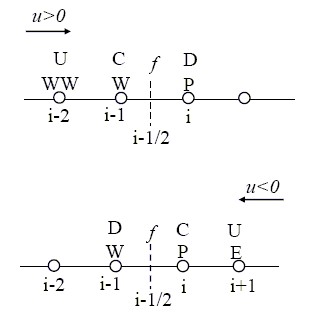
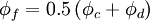
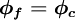
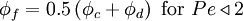
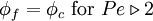

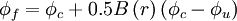
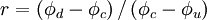
![B\left( r \right) = 0.5 \left[ \left( 1 + \kappa \right) r + \left( 1 - \kappa \right) \right]](/W/images/math/2/5/2/252fde838ad2c7179503629ccc7513b3.png)
![f_{w}=f_{C}+ \frac{1}{4}\left[\left( 1+\kappa \right)\left(f_{D}-f_{C}\right)+\left(1-\kappa \right) \left( f_{D}-f_{U} \right)\right]](/W/images/math/8/6/f/86f2cf8f35978278fb5e1cd5f2071fc4.png)
![\hat{f_{w}}=\hat{f_{w}}+\frac{1}{4}
\left[\left( 1+\kappa \right)\left( 1-\hat{f_{C}}\right)+
\left( 1-\kappa \right)\hat{f_{C}}\right]](/W/images/math/a/d/3/ad34e6d6bdcfc12041ddae6c26dd78f1.png)