2-D vortex in isentropic flow
From CFD-Wiki
This is one of the few exact solutions for the compressible Euler equations. The test case involves convection of an isentropic vortex in inviscid flow. It is used to show the ability of numerical schemes to accurately capture vortical flows. The free-stream conditions are
Perturbations are added to the free-stream in such a way that there is no entropy gradient in the flow-field. The perturbations in the velocity are given by:
![(\delta u, \delta v) = \frac{\beta}{2\pi} \exp\left( \frac{1-r^2}{2}
\right) [ -(y-y_o), (x-x_o) ]](/W/images/math/b/f/4/bf4d03266bdcc72a5731401a2efc95dc.png)
while the temperature, density and pressure are given by
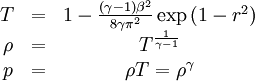
where
is distance from the vortex center 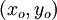 .
.
One choice for the domain and parameters is:
As a result of isentropy, the exact solution corresponds to a pure advection of the vortex at the free-stream velocity. This problem is usually solved with periodic boundary conditions. Further details can be found in Yee et al. (1999).
References
- Yee, H-C., Sandham, N. and Djomehri, M., (1999), "Low dissipative high order shock-capturing methods using characteristic-based filters", JCP, Vol. 150.

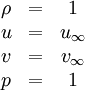
![r = [ (x-x_o)^2 + (y-y_o)^2 ]^{1/2}](/W/images/math/6/3/5/635b76a00e794bbe4119341445847905.png)
![\Omega = [0,10] \times [-5,5], \quad
(x_o, y_o) = (5,0), \quad
\beta = 5](/W/images/math/c/e/a/ceae1619f8ff0db839e9a7afecbd5f9c.png)