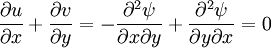Stream function
From CFD-Wiki
(Difference between revisions)
m |
|||
| Line 3: | Line 3: | ||
On a streamline in two-dimensional flow | On a streamline in two-dimensional flow | ||
| - | <math> | + | :<math> |
d\psi = \frac{\partial \psi}{\partial x} dx + \frac{\partial \psi}{\partial y} dy = 0 | d\psi = \frac{\partial \psi}{\partial x} dx + \frac{\partial \psi}{\partial y} dy = 0 | ||
</math> | </math> | ||
| Line 9: | Line 9: | ||
The equation of a streamline in two-dimensions is | The equation of a streamline in two-dimensions is | ||
| - | <math> | + | :<math> |
v dx - u dy = 0 | v dx - u dy = 0 | ||
</math> | </math> | ||
| Line 15: | Line 15: | ||
Comparing the two equations, we have | Comparing the two equations, we have | ||
| - | <math> | + | :<math> |
u = - \frac{\partial \psi}{\partial y} | u = - \frac{\partial \psi}{\partial y} | ||
</math> | </math> | ||
| - | <math> | + | :<math> |
v = \frac{\partial \psi}{\partial x} | v = \frac{\partial \psi}{\partial x} | ||
</math> | </math> | ||
| Line 25: | Line 25: | ||
Conversely, the stream function at any point <math>P</math> can be obtained from the velocity field by a line integral | Conversely, the stream function at any point <math>P</math> can be obtained from the velocity field by a line integral | ||
| - | <math> | + | :<math> |
\psi(P) = \psi(P_o) + \int_{P_o}^P [ v(x,y,t) dx - u(x,y,t) dy ] | \psi(P) = \psi(P_o) + \int_{P_o}^P [ v(x,y,t) dx - u(x,y,t) dy ] | ||
</math> | </math> | ||
| Line 33: | Line 33: | ||
If the flow is incompressible, then the continuity equation is identically satisfied | If the flow is incompressible, then the continuity equation is identically satisfied | ||
| - | <math> | + | :<math> |
\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = -\frac{\partial^2 \psi}{\partial x \partial y} + \frac{\partial^2 \psi}{\partial y \partial x} = 0</math> | \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = -\frac{\partial^2 \psi}{\partial x \partial y} + \frac{\partial^2 \psi}{\partial y \partial x} = 0</math> | ||
Latest revision as of 11:39, 12 September 2005
The stream function is a scalar field variable which is constant on each streamline. It exists only in two-dimensional and axisymmetric flows.
On a streamline in two-dimensional flow
The equation of a streamline in two-dimensions is
Comparing the two equations, we have
Conversely, the stream function at any point 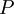 can be obtained from the velocity field by a line integral
can be obtained from the velocity field by a line integral
where 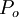 is some reference point and one can assume
is some reference point and one can assume 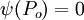 since the stream function is determined only upto a constant.
since the stream function is determined only upto a constant.
If the flow is incompressible, then the continuity equation is identically satisfied

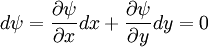
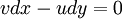
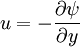
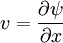
![\psi(P) = \psi(P_o) + \int_{P_o}^P [ v(x,y,t) dx - u(x,y,t) dy ]](/W/images/math/0/6/1/061c8e98a4c2cb20abf21f9183e0332e.png)