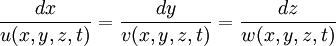Streamline
From CFD-Wiki
(Difference between revisions)
m (Stream line moved to Streamline) |
m |
||
| Line 1: | Line 1: | ||
A line in the fluid whose tangent is everywhere parallel to the local velocity vector <math>(u,v,w)</math> instantaneously is a streamline. The family of streamlines at time <math>t</math> are solutions of | A line in the fluid whose tangent is everywhere parallel to the local velocity vector <math>(u,v,w)</math> instantaneously is a streamline. The family of streamlines at time <math>t</math> are solutions of | ||
| - | <math> | + | :<math> |
\frac{dx}{u(x,y,z,t)} = \frac{dy}{v(x,y,z,t)} = \frac{dz}{w(x,y,z,t)} | \frac{dx}{u(x,y,z,t)} = \frac{dy}{v(x,y,z,t)} = \frac{dz}{w(x,y,z,t)} | ||
</math> | </math> | ||
Revision as of 11:39, 12 September 2005
A line in the fluid whose tangent is everywhere parallel to the local velocity vector  instantaneously is a streamline. The family of streamlines at time
instantaneously is a streamline. The family of streamlines at time 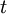 are solutions of
are solutions of
Streamlines cannot intersect since the velocity at any point is unique.
In two dimensions and for axisymmetric flows, a stream function exists which is constant on each streamline.