 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
saeid kheradmand
Join Date: Mar 2009
Posts: 13
Rep Power: 17  |
Dear all,
I am going to add Nox prediction (zeldowich) to achen bomb. Is it neccessary to edit the source code? (is it possible by just editing dictionaries?) thank you for your time. regards saeid |
|
|
|

|
|
|
|
|
#2 |
|
Super Moderator
Niklas Nordin
Join Date: Mar 2009
Location: Stockholm, Sweden
Posts: 693
Rep Power: 29   |
This is a very weird question.
You are going to add a NOx mechanism to a case??? So will you be able to use it on only the aachen bomb case then? Anyways..... If you are planning to use dieselFoam, then you will use the chemkin-interface and in that case it has already been done. If you look at the mechanism chem.inp_15 you'll find its already in there. |
|
|
|

|
|
|
|
|
#3 |
|
New Member
saeid kheradmand
Join Date: Mar 2009
Posts: 13
Rep Power: 17  |
Dear Dr Nordin
Thank you for your answer I dont want to use mechanism like chem.inp-15 (I have used it and it worked). I am going to use a one step reaction fuel+oxidant=co2+h2o and a simplified Nox mechanism that d(NO)/dt depeneds on O2 and N2. sorry for the weird questions(cases like achen bomb) regards saeid |
|
|
|

|
|
|
|
|
#4 |
|
Super Moderator
Niklas Nordin
Join Date: Mar 2009
Location: Stockholm, Sweden
Posts: 693
Rep Power: 29   |
Ok, so you do not want to use Zeldovich,
since you're planning to bolt on NOx to the global fuel conversion rate. Then I'd suggest you just use 2 reactions in chem.inp. one for the fuel conversion rate and one for the NO, like NO + NO = N2 + O2 |
|
|
|

|
|
|
|
|
#5 |
|
New Member
saeid kheradmand
Join Date: Mar 2009
Posts: 13
Rep Power: 17  |
thank you very much.
I will do that and compare with complex mechanism. than you |
|
|
|

|
|
|
|
|
#6 |
|
New Member
baran
Join Date: Aug 2013
Posts: 5
Rep Power: 13  |
how to calculate fuel nox in openfoam
|
|
|
|

|
|
|
|
|
#7 |
|
New Member
Ali Kadar
Join Date: Oct 2014
Location: Delft
Posts: 25
Rep Power: 12  |
Hello everyone,
I would like to post-process NOx formation by considering only the global species concentrations for 1-step irreversible methane combustion. From what I have understood and read I came to the following conclusion. The formation of thermal 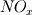 according to the extended Zeldovich mechanism is given by according to the extended Zeldovich mechanism is given by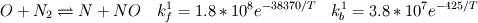 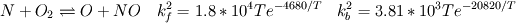 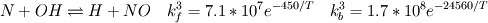 with rate constants in 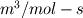 The rate of formation of [NO] is then given by ![\frac{d[NO]}{dt} \: = \: k_f^1 [O] [N_2] + k_f^2 [N] [O_2] + k_f^3 [N] [OH] - k_r^1 [NO] [N] - k_r^2 [NO] [O] - k_r^3 [NO] [H] \frac{d[NO]}{dt} \: = \: k_f^1 [O] [N_2] + k_f^2 [N] [O_2] + k_f^3 [N] [OH] - k_r^1 [NO] [N] - k_r^2 [NO] [O] - k_r^3 [NO] [H]](/Forums/vbLatex/img/74fc0df7514c1afa15a94ba2b2379bd9-1.gif) which under the quasi-steady assumption for [N] can be simplified to ![\frac{d[NO]}{dt} \quad = \quad 2 \: k_f^1 \: [O] \: [N_2] \quad \frac{\left(1-\frac{k_b^1 \: k_b^2 \: {[NO]}^2}{k_f^1 \: [N_2] \: k_f^2 \: [O_2]}\right)}{\left(1+\frac{k_r^1 \: [NO]}{k_f^2 \: [O_2] \: + \: k_f^3 \: [OH]}\right)} \quad (mol/m^3-s) \frac{d[NO]}{dt} \quad = \quad 2 \: k_f^1 \: [O] \: [N_2] \quad \frac{\left(1-\frac{k_b^1 \: k_b^2 \: {[NO]}^2}{k_f^1 \: [N_2] \: k_f^2 \: [O_2]}\right)}{\left(1+\frac{k_r^1 \: [NO]}{k_f^2 \: [O_2] \: + \: k_f^3 \: [OH]}\right)} \quad (mol/m^3-s)](/Forums/vbLatex/img/7c13b71932be9e7b542de4818d251efc-1.gif) with equilibrium concentration of [O] given by ![[O] = 3.97*10^5 T^{-1/2} e^{-31090/T}\: [O_2]^{1/2} mol/m^3 [O] = 3.97*10^5 T^{-1/2} e^{-31090/T}\: [O_2]^{1/2} mol/m^3](/Forums/vbLatex/img/a4ce43a4524d6423832176c2fdbf9d04-1.gif) and the concentration of [OH] is given by ![[OH] = 2.129*10^2 \: T^{-0.57} \: e^{-4595/T} \: [O]^{1/2} \: [H_2O]^{1/2} mol/m^3 [OH] = 2.129*10^2 \: T^{-0.57} \: e^{-4595/T} \: [O]^{1/2} \: [H_2O]^{1/2} mol/m^3](/Forums/vbLatex/img/4a1b7b0013f654513d3efb13e017e799-1.gif) using partial equilibrium approach. using partial equilibrium approach.Therefore, the concentration of [NO] can be obtained by solving the following scalar transport equation with ![\phi = [NO] \phi = [NO]](/Forums/vbLatex/img/02c6982a91ef9f0bc25af6d1f69950b4-1.gif) and and ![S_{[NO]} = M_{NO} \frac{d[NO]}{dt} S_{[NO]} = M_{NO} \frac{d[NO]}{dt}](/Forums/vbLatex/img/2487bdf7cda12ed31abb4e02c1c75c67-1.gif) 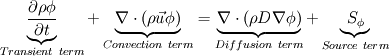 So, basically to successfully post-process NOx formation in OpenFOAM we need to solve the scalar transport equation for [NO] with a spatially varying source term which depends upon the concentration of [NO]. Can someone suggest a possible way of doing this. This is a non linear equation and would need to be solved iteratively. I want to implement this in OF but do not know where to start from. Any ideas please ??
__________________
A good solution is one which does justice to the inner nature of the problem- Cornelius Lanczos in a letter to Albert Einstein on March 9, 1947 |
|
|
|

|
|
|
|
|
#8 |
|
New Member
Ali Kadar
Join Date: Oct 2014
Location: Delft
Posts: 25
Rep Power: 12  |
Hello, I have successfully implemented thermal NOx formation using scalarTransportFoam. The results are qualitatively very good when compared to Fluent, however quantitatively they differ by a constant factor. I am not able to understand where I go wrong. Any suggestions ??
__________________
A good solution is one which does justice to the inner nature of the problem- Cornelius Lanczos in a letter to Albert Einstein on March 9, 1947 |
|
|
|

|
|
|
|
|
#9 | |
|
Member
Arvind Jay
Join Date: Sep 2012
Posts: 97
Rep Power: 15  |
Quote:
|
||
|
|

|
||
|
|
|
#10 |
|
Senior Member
Reviewer #2
Join Date: Jul 2015
Location: Knoxville, TN
Posts: 141
Rep Power: 11  |
Quote:
I ran into similar problems. I post some lesson learned for people like me who was not familiar with the reaction modeling. An immediate and easy implementation is just using the concentration of [NO] of previous to calculation the source term and then solve the transport equation. If this is how the solver implemented, then the solver may have some potential issue. Typically, I found the reliable solution requires very small time step ~1e-4. This limited by the reaction term. So here is what is typically done in a spirit of time split scheme to couple the transport and reaction at a different times scales 1. First, solve the nonlinear (can be stiff) ODE of the source/sink term of d[NO]/dt = f (NO). The ODE solves that implemented in OpenFOAM can be used. Notice this step, one may want the ODE to be solved with some accuracy. For low order explicit scheme, most time, it takes large number of time step to solve this ODE within certain accuracy. 2. Once you solve the ODE you will have the concentration at new time [NO]_n+1. Then the sink term can be estimated as ([NO]_n+1 - [NO]_n)/ deltaT. Plug this term into the scalarTransport and solve the transport equation. 3. Iterate above steps. Note that with time split, the solution should allow a much large time step. However, depends on the problem and treatment of the time split scheme (i.e., order accuracy), one may still need some fair small time step. A good discussion on the different split schemes can be found in this conference paper https://arc.aiaa.org/doi/10.2514/6.2020-2139 Also, there is very good discussion in another post: Numerical treatment of the source term in combustion equations Thanks, Rdf Last edited by randolph; September 15, 2020 at 14:02. Reason: add reference |
|
|
|

|
|
 |
|
|