 |
|
|
[Sponsors] | |||||
WENO scheme validation - rhoCentralFoam - shockTube/Shu-Osher problems |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Join Date: Sep 2015
Location: Singapore
Posts: 102
Rep Power: 11  |
Dear all,
I have implemented an n-th order WENO scheme in OpenFOAM and modified the rhoCentralFoam solver (with TVD 3rd order RK time marching). I have simulated both the shockTube and the Shu-Osher problems. The solution for the shockTube problem looks fine for both the 5th and 7th order WENO schemes. However, small wiggles occur near the small shocklets for the Shu-Osher problem. So far, I have not seen anybody reporting about this problem. I have no idea why this is happening. Has anyone faced this problem or something similar to this when implementing WENO schemes? With many thanks, USV |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Sep 2015
Location: Singapore
Posts: 102
Rep Power: 11  |
Dear all,
I managed to eliminate the oscillations but I have no idea why it works. I just want to give more information so that someone might be able to help me understand. First of all, previously, I was reconstructing 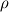 , ,  and and 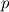 using the WENO scheme. Then, I applied the HLL flux at the interface which led to the oscillations for the Shu-Osher test case. using the WENO scheme. Then, I applied the HLL flux at the interface which led to the oscillations for the Shu-Osher test case.Today, I modified the code using the method described here. Basically, instead of reconstructing the flow variables  , the fluxes , the fluxes  were reconstructed from the left and right sides, respectively. were reconstructed from the left and right sides, respectively.![\textbf{q} = \left[ \rho, \rho{}u, \rho{}E \right] \textbf{q} = \left[ \rho, \rho{}u, \rho{}E \right]](/Forums/vbLatex/img/f261a91aa0c1b7ec425aa6f4b18a83ac-1.gif) ![\textbf{F}^{\pm} (\textbf{q}) = \left[ \rho{}u, \rho{}u^2 + p, (\rho{}E +p)u \right] \pm a_{max} \textbf{q} \textbf{F}^{\pm} (\textbf{q}) = \left[ \rho{}u, \rho{}u^2 + p, (\rho{}E +p)u \right] \pm a_{max} \textbf{q}](/Forums/vbLatex/img/2138b04907846f0b46efa9fcdffeec20-1.gif) Then, the Lax–Friedrichs (LxF) numerical flux was defined as: ![\textbf{F}_{1/2} = \frac{1}{2} \left[ \textbf{F}_{1/2}^{+} + \textbf{F}_{1/2}^{-} \right] \textbf{F}_{1/2} = \frac{1}{2} \left[ \textbf{F}_{1/2}^{+} + \textbf{F}_{1/2}^{-} \right]](/Forums/vbLatex/img/cff61cfc3ae95cebffa9f3c3b4bee4b7-1.gif) This appears to have solved the problem of the oscillations that I mentioned in the previous post. However, I am at a loss as to why WENO-reconstructing [MATH]\textbf{q}[\MATH] and computing an upwind-biased numerical flux (e.g. HLL, HLLC) leads to oscillations. I will be grateful if anyone could explain how to properly implement the HLL numerical flux scheme in this case. With many thanks, USV |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Join Date: Sep 2015
Location: Singapore
Posts: 102
Rep Power: 11  |
Dear all,
I would like to report on a (known) solution for this problem. Apparently, WENO schemes can be oscillatory when used to reconstruct primitive or conservative variables but not so when used to reconstruct characteristic variables. A friend of mine coded WENO7 with HLL flux separately in Matlab and found that it led to the same oscillations as OpenFOAM. He further went to code WENO7 with characteristic variables and found that the oscillations did not appear. However, he also commented that the computation time was 3-5 times longer even for a specialized 1D case. USV |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Frank Ann
Join Date: Dec 2016
Posts: 6
Rep Power: 10  |
Hi usv,
I want to implement a high-order difference scheme in openfoam too, can you tell me that how did you implement WENO in openfoam? The RK time scheme is accomplished by modified the solver, how about weno scheme? I will be grateful if you could share it or give me some advice. Thanks! Regards, ajog Last edited by ajogajog; September 10, 2017 at 08:10. |
|
|
|

|
|
|
|
|
#5 | |
|
Senior Member
Join Date: Sep 2015
Location: Singapore
Posts: 102
Rep Power: 11  |
Quote:
I developed a finite volume (FV) formulation since OpenFOAM is based on that. I am sorry that I can't share the code (yet) but I can give you some details. First of all, you need to build the stencils. If you intend to use a finite difference (FD) formulation, then you are probably assuming that cell values represent the point values at the cell centres. So, there will be a stencil for each cell. Unless you have a structured mesh consisting of a single block, the ordering of cells in OpenFOAM does not follow any particular pattern which you can exploit to avoid building the stencils. Secondly, since you intend to use a finite difference (FD) formulation, I am going to assume that your mesh is Cartesian and uniform. In that case, you can follow any standard paper on WENO for the reconstruction coefficients, smoothness indicators, linear weights, etc. The simplicity of the mesh means that you can hard code these as functions that you use in the solver. If your mesh is non-uniform, then each cell/stencil will have its own set of reconstruction coefficients, smoothness indicators, linear weights, etc. That will be harder to implement. Thirdly, you'll need to figure out how you're going to treat the boundaries. Periodic boundaries have the advantage of not requiring any ghost cell treatment (but will require some clever coding). If you have other types of boundaries, you can choose to adopt the ghost cell method or reduce the order of reconstruction close to the boundaries. Lastly, I suggest that you begin from 1D problems and work your way up to higher dimensions. USV |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [ICEM] Problems with coedge curves and surfaces | tommymoose | ANSYS Meshing & Geometry | 6 | December 1, 2020 12:12 |
| Problems adding volScalarField to rhoCentralFoam | cryple | OpenFOAM Programming & Development | 2 | January 17, 2013 06:18 |
| [GAMBIT] Problems with the Cooper Scheme | Forrest | ANSYS Meshing & Geometry | 0 | July 13, 2009 11:59 |
| Help for cut cell scheme for moving problems | Wei | Main CFD Forum | 0 | August 2, 2006 10:32 |
| Implicit scheme for incompressible flow problems | Triton | Main CFD Forum | 4 | August 25, 2002 05:54 |