 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
X
Join Date: Jan 2019
Posts: 63
Rep Power: 7  |
Hello.
I need some guidance with writing equations in my header file. I am working on electrohydrodynamic (EHD) solver that uses interFoam+electrostatics elements (http://openfoamwiki.net/index.php/Co...ectromagnetics) As you can see from the above link, the third equation that is the charge conservation equation is written as (the two equations are the same where 1st one is used in the link above and the other one is the same but written using different variables). Screenshot 2021-02-17 174400.png In my header file, I have written Code:
tmp<fvScalarMatrix> ECDEqn
(
fvm::ddt(rhoE)
- fvc::laplacian(sgm, Ue)
+ fvm::div(phi, rhoE)
);
solve(ECDEqn);
where K is equivalent to the previous equation's sigma. I have tried rewriting my header file equation but only this seems to be working. Is it correct? Code:
tmp<fvScalarMatrix> ECDEqn
(
fvm::laplacian(sgm, Ue)
);
solve(ECDEqn);
Can someone guide me on how to write the simplified equation? Many thanks [1] https://iopscience.iop.org/article/1...17/23/1/015004 Last edited by mcfdma; February 18, 2021 at 03:45. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 746
Rep Power: 14  |
Umm ... I am struggling to relate your coding to your equations. Just for clarity:
Code:
tmp<fvScalarMatrix> ECDEqn
(
fvm::ddt(rhoE)
- fvc::laplacian(sgm, Ue)
+ fvm::div(phi, rhoE)
);
solve(ECDEqn);
 or perhaps the following if the code takes an incompressible flow approach (  ): ): which is probably not what you are after ... or is it? If not, then it's probably a good idea to read up on the meaning of laplacian & div. Good luck my friend. |
|
|
|

|
|
|
|
|
#3 |
|
Member
X
Join Date: Jan 2019
Posts: 63
Rep Power: 7  |
Many thanks for your reply. Yes, I am aware of laplacian and divergence.
I believe I made a blunder mistake in writing my second equation (Apologies):  and   Using Gauss Law  along with along with  I get,  Code:
tmp<fvScalarMatrix> ECDEqn
(
fvm::ddt(rhoE)
+ fvm::div(phi, rhoE)
- fvc::laplacian(sgm, Ue)
);
solve(ECDEqn);
 Have I done anything wrong? I have been getting appropriate results but wanted to implement this simplified part,  to observe the change but wanted to know if what I had written was correct. Code:
tmp<fvScalarMatrix> ECDEqn
(
fvm::laplacian(sgm, Ue)
);
solve(ECDEqn);
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 746
Rep Power: 14  |
Aaah - that makes sense now, and yes your coding looks good to me.
In case you are interested, the difference between fvm and fvc is subtle: fvm builds the matrix coefficients for an implicit representation of the term (i.e. expresses the equation in terms of the variable at the new time step), whilst fvc uses an explicit representation (using old time values only) ... so it makes sense that at least one of your terms in the fvMatrix must be an implicit (fvm) term. |
|
|
|

|
|
|
|
|
#5 |
|
Member
X
Join Date: Jan 2019
Posts: 63
Rep Power: 7  |
Thanks for the quick fvm and fvc explanation.
Could I double check when you say my coding looks okay, do you mean the original equation with 3 terms or the simplified one or all of them? |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 746
Rep Power: 14  |
Both look fine to me - did they compile and run okay?
|
|
|
|

|
|
|
|
|
#7 |
|
Member
X
Join Date: Jan 2019
Posts: 63
Rep Power: 7  |
Thanks for the quick response, much appreciated.
Yes, it does compile alright but since the original equation has now been simplified, I have run a case but there has been no charge density  at that surface of the fluid. I am left confused which is why I posted thinking I made a mistake in my coding. at that surface of the fluid. I am left confused which is why I posted thinking I made a mistake in my coding.Would it be possible for you to have a quick look at my solver? |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 746
Rep Power: 14  |
By all means, I can take a look at your code, although it has been 30yrs or so since I did my course on electromagnetism!
I would suggest checking your logic first, though. Note that your second (simplified) equation just calculates a divergence-free  field, but you stated earlier that: field, but you stated earlier that: and so does this not constrain the charge density  to zero? Perhaps I am missing something. to zero? Perhaps I am missing something.Note also that I am assuming that variables  and and 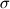 are constants, since you are moving them inside and outside of the integrals. are constants, since you are moving them inside and outside of the integrals.
|
|
|
|

|
|
|
|
|
#9 |
|
Member
X
Join Date: Jan 2019
Posts: 63
Rep Power: 7  |
Thank you very much
 30 years? wow, that's amazing! 30 years? wow, that's amazing! This part is correct  but your equation ending with equals to 0 should be for the simplified equation including conductivity  This above equation is the leaky-dielectric model. I have created a dropbox link that contains my actual solver (not the leaky-dielectric model). You are absolutely correct, I am assuming these 2 parameters  and and 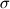 constant along with the surface tension at the interface. constant along with the surface tension at the interface.
|
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 746
Rep Power: 14  |
I am probably missing something here, but let me try reiterating my above point. We start with the charge conservation equation:
  where D/Dt is the material derivative since the fluid is incompressible; and then you want to set:  which means that:  i.e. the charge density field will be unchanging, or at least is just convected through the domain if the inlet boundary boundary value is non-zero. Indeed, looking briefly at your EHDEqn.H code, the ECDEqn is where the rhoE value is calculated/updated and so if you change this to your new, simplified version of the equation then where is rhoE calculated now? It is probably just remaining at its initial field definition. You would need to add another expression to calculate rhoE from the electric field since the EHD equation no longer solves for rhoE. Does that explain why you are not seeing any charge density when you use this simplified version? I don't have access to the paper that you referenced at the start, nor to your model BCs, but I would suggest thinking again about those to make sure that the simplified equation makes sense for your application, and that your BCs are correct. Good luck. |
|
|
|

|
|
 |
| Tags |
| ehd, ehdfoam, electrospray |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Solving coupled steady and unsteady equation in OpenFOAM | jd87 | OpenFOAM Running, Solving & CFD | 2 | July 22, 2020 12:36 |
| mass flow in is not equal to mass flow out | saii | CFX | 12 | March 19, 2018 06:21 |
| Some problem of "Qcriterion.mcr& | yuyuxuan | Tecplot | 9 | February 12, 2016 04:27 |
| Need help:about energy equation in CFX | Stein | CFX | 4 | July 2, 2009 23:31 |
| Diffusion Equation | izardy amiruddin | Main CFD Forum | 2 | July 4, 2002 09:14 |