 |
|
|
[Sponsors] | |||||
Crank Nicolson scheme implemented wrong? |
 18Likes
18Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Rajib Roy
Join Date: Jun 2014
Location: Laramie, Wyoming
Posts: 18
Rep Power: 12  |
Edit 2: 2020 May 04
OpenFOAM CrankNicolson implementation is correct when at each time step the linear system residual is zero. For derivation, please see forum post 10. Original post: The Crank-Nicolson temporal discretization scheme for any variable 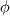 is defined as is defined as  , where , where 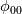 is the is the 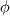 value two time-steps earlier. value two time-steps earlier.There is potential error in OpenFOAM v7 CrankNicolsonDdtScheme implementation. The off-center coefficient for blending with Euler implicit scheme is defined as Code:
ddtSchemes
{
default CrankNicolson ocCoeff; // ocCoeff [0, 1]
}
Code:
cnCoeff = 1.0/(1.0 + ocCoeff); However, within the implementation cnCoeff is not declared/defined, and a separate variable coef defined as Code:
coef_ = 1 + ocCoeff; Let us investigate how this apparent bug affects the discretization scheme (for fvcDdt member function and mesh not moving): Code:
//- Off-centering coefficient function // 1 -> CN, less than one blends with EI autoPtr<Function1<scalar>> ocCoeff_; //- Return the coefficient for Euler scheme for the first time-step // for and CN thereafter coef_ = 1 + ocCoeff(); //- Return the reciprocal time-step coefficient for Euler for the // first time-step and CN thereafter rDtCoef_ = coef_/deltaT(); //- Return ddt0 multiplied by the off-centreing coefficient offCentre_(ddt0()) = ocCoeff()*ddt0; // previous temporal derivative ddt0 = rDtCoef0_(ddt0)*(vf.oldTime() - vf.oldTime().oldTime()) - offCentre_(ddt0()); // explicit temporal derivative calculation fvcDdt(vf) = rDtCoef*(vf - vf.oldTime()) - offCentre_(ddt0()) Code:
fvcDdt(vf) = (1 + ocCoeff) * (vf - vf.oldTime())/deltaT - ocCoeff * fvcDdt(vf.oldTime())  Approximating the earlier temporal derivative as implicit Euler Code:
fvcDdt(vf.oldTime()) = (vf - vf.oldTime())/deltaT0 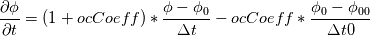 For uniform time step, the standard Crank Nicolson scheme (ocCoeff = 1) becomes  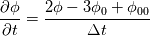 , which is very different from Crank Nicolson scheme. , which is very different from Crank Nicolson scheme.This could be solved if the cnCoeff is used instead of coeff!  With uniform time step, the standard Crank Nicolson scheme (ocCoeff = 1) can be written as  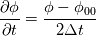 I have confidence in my own analysis, but it is hard to believe OpenFOAM developers and users missed such a crucial bug. I will be happy to proven wrong! Please review, and am looking forward to your feedback! Edit: For (ocCoeff = 0.5), the scheme becomes: OpenFOAM implementation:   Proposed correction:  
Last edited by rajibroy; May 4, 2020 at 21:03. Reason: Edit 1: Added an example; Edit 2: OF CN scheme is correct (see post 10) |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Rajib Roy
Join Date: Jun 2014
Location: Laramie, Wyoming
Posts: 18
Rep Power: 12  |
To verify the Crank-Nicolson scheme, we can printout the the discretization coefficients:
Code:
template<class Type>
tmp<fvMatrix<Type>>
CrankNicolsonTestDdtScheme<Type>::fvmDdt
(
const GeometricField<Type, fvPatchField, volMesh>& vf
)
{
.
.
.
Info << "deltaT" << deltaT()
<< "\tocCoeff: " << ocCoeff()
<< ",\tcoef: " << coef_(ddt0)
<< ",\trDtCoef: " << rDtCoef
// << ",\trDtCoef0: " << rDtCoef0_(ddt0).value()
<< endl;
}
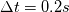 , the OF v7 implementation provides: , the OF v7 implementation provides:Code:
deltaT: 0.2 ocCoeff: 0.5, coef: 1.5, rDtCoef: 7.5, For corrected implementation, the coefficients are: Code:
deltaT: 0.2 cnCoeff: 0.67 coefft: 0.67 coefft0: -0.33 coefft00: -0.33, |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Rajib Roy
Join Date: Jun 2014
Location: Laramie, Wyoming
Posts: 18
Rep Power: 12  |
The Crank Nicolson implementation in OpenFOAM uses previous temporal derivative
 instead of instead of 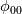 . Either way, the scheme need to store an additional field. There is no additional benefit of saving . Either way, the scheme need to store an additional field. There is no additional benefit of saving  , although it may lead to potential inaccurate temporal derivative! , although it may lead to potential inaccurate temporal derivative! Here is how (simplified using uniform time step and ocCoef): OF Crank-Niconson implementation   Similarly, the 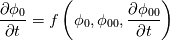 . .Thus, at any time step n, the temporal derivative involves all phi values from 0 to n.  which is clearly a deviation from Crank-Nicolson discrete temporal discretization scheme. |
|
|
|

|
|
|
|
|
#4 |
|
Member
Rodrigo
Join Date: Mar 2010
Posts: 98
Rep Power: 16  |
Hi Rajib,
Did you think about bringing this up to the development team? https://bugs.openfoam.org/rules.php It may turn out that this deviation from original Crank-Nicolson was accidental or even prosecuted. Either the way, clearing this may be in benefit for the OF-community. Hint: You will be probably asked for a case or a reproducible set of instructions that probe this deviated behaviour. Best & thanks for your effort! |
|
|
|

|
|
|
|
|
#5 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Dear Rajib,
first of all, thank you for your clear post and the usage of code tags. Your hints are clear and we can easily follow. I checked the code just the last 5 minutes but I cannot dive into that scheme right now for two reasons:
As far as I remember, the Crank Nic. scheme uses the actual and old value. Regarding the coefficient. I need to find some reference for that.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Rajib Roy
Join Date: Jun 2014
Location: Laramie, Wyoming
Posts: 18
Rep Power: 12  |
Hello Tobi,
I have implemented the Crank-Nicolson scheme following the explanation in the section 13.3..5, page 512 of the book Moukalled, F., Mangani, L., & Darwish, M. (2015). The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM® and Matlab. https://doi.org/10.1007/978-3-319-16 If you need a copy of the chapter, could you please pm an email address? If you come across references for CrankNicolson scheme for FVM implementation, would you please post in the thread? --------------------------------------------------------------------------- Hello Rodrigo, Thank you for your kind suggestion. Prior to reaching out to the OF developers, I am reaching out to the community users to get feedback so that bug report is comprehensive. Regarding a test case, I might need to develop a one-dimensional wave equation. Your kind suggestion is much appreciated. Thanks again both of you! Regards, Rajib |
|
|
|

|
|
|
|
|
#7 |
|
New Member
Rajib Roy
Join Date: Jun 2014
Location: Laramie, Wyoming
Posts: 18
Rep Power: 12  |
A 1D scalar transport equation is used to verify the temporal discretization schemes, where a passive scalar (phi) is convected along the Cartesian x-axis using a uniform flow velocity of (1, 0, 0):
The schemes used for temporal discretization are:  Domain extends [0,1] in a Cartesian XY plane. A sinusoidal field ![[ \phi (y) = sin(2 \pi y) ] [ \phi (y) = sin(2 \pi y) ]](/Forums/vbLatex/img/fe2a2d1572483efe34a049c3a9a2bab8-1.gif) is applied on the left (x = 0) at time 0, and convected toward the right (along x axis). is applied on the left (x = 0) at time 0, and convected toward the right (along x axis).    After 1 characteristic time, scalar field values are plotted along line 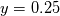 , which is analytically 1. The scheme comparison plot is attached. , which is analytically 1. The scheme comparison plot is attached.Analysis: The CrankNicolson scheme implemented in OpemFOAM is behaving oscillatory similar to the 2nd order upwind (aka backward) scheme. The modified Crank-Nicolson (CNMod) scheme implemented by the author (as described in the first post) is oscillation free. However, the modified Crank-Nicolson scheme have the same accuracy as the Euler scheme. I was expecting better accuracy form the CNMod scheme. The case study is available at GitHub https://github.com/rroyCFD/temporalD...rification.git Please review and I look forward to your comments. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Herpes Free Engineer
Join Date: Sep 2019
Location: The Home Under The Ground with the Lost Boys
Posts: 931
Rep Power: 13  |
is there any chance for you to report your findings in the issue tracker of one of the OpenFOAM variants? links below may guide you.
__________________
The OpenFOAM community is the biggest contributor to OpenFOAM: User guide/Wiki-1/Wiki-2/Code guide/Code Wiki/Journal Nilsson/Guerrero/Holzinger/Holzmann/Nagy/Santos/Nozaki/Jasak/Primer Governance Bugs/Features: OpenFOAM (ESI-OpenCFD-Trademark) Bugs/Features: FOAM-Extend (Wikki-FSB) Bugs: OpenFOAM.org How to create a MWE New: Forkable OpenFOAM mirror |
|
|
|

|
|
|
|
|
#9 |
|
New Member
Rajib Roy
Join Date: Jun 2014
Location: Laramie, Wyoming
Posts: 18
Rep Power: 12  |
After further study, I realized that any temporal discretization scheme shall be discussed in conjunction with explicit/implicit treatment of the spatial discretization operators.
The Crank-Nicolson (CN) scheme implementation in OpenFOAM doesn't interact with spatial discretization operators. Hence, the CN scheme can't be applied in the default solvers (i.e. the user have to modify the momentum/transport equation of the solvers). The two types of CN schemes are:  and 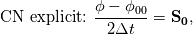 where  is spatial discretization operator. is spatial discretization operator.If we introduce, a CN coefficient (off-center coefficient > ocCoeff) from blending with implicit Euler scheme, the reformulated schemes will be: ![ocCoef \in [1, 0] \quad 1: \text{semi-Implicit CN} \quad 0: \text{implicit Euler} ocCoef \in [1, 0] \quad 1: \text{semi-Implicit CN} \quad 0: \text{implicit Euler}](/Forums/vbLatex/img/66c5a5cffe573709a822342ed4a47d70-1.gif) ![cnCoef = \frac{1}{1 + ocCoef}; \quad ocCoef \in [0.5, 1] cnCoef = \frac{1}{1 + ocCoef}; \quad ocCoef \in [0.5, 1]](/Forums/vbLatex/img/eb43522ae3596458beb7f2ae565c1447-1.gif)  The correction I proposed in the earlier post, following the OpenFOAM implementation, is neither semi-implicit nor explicit. The implementation intended to blend temporall discretization operators of the explicit CN and implicit Euler schemes while all spatial operators are treated as implicit (where possible). Please find the attached plot of the scalar transport of the sinusoidal wave. The explicit CN scheme is not stable (super oscillatory) in absence of diffusivity (thus not plotted). Both inaccurate OpenFOAM implementation and semi-implicit implementation of the CN scheme give same result as the backward scheme (which might misled the OF developers). I look forward to your comments, and planning to submit a bug report with OpenFOAM. |
|
|
|

|
|
|
|
|
#10 |
|
New Member
Rajib Roy
Join Date: Jun 2014
Location: Laramie, Wyoming
Posts: 18
Rep Power: 12  |
The Crank-Nicolson temporal discretization scheme can be viewed as summation of implicit and explicit Euler discretization schemes.
For any variable 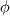 , let assume the linear system for the partial differential equation is written as: , let assume the linear system for the partial differential equation is written as: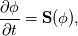 where  is the spatial discretization operator. is the spatial discretization operator.The temporal derivatives can discretized as : Implicit Euler 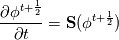  Explicit Euler   Crank Nicolson Adding equations {Eqn:implEuler} and {Eqn:explEuler}, we get 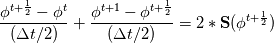 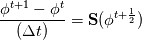 With central difference approximation for  , the final form of the discretization becomes: , the final form of the discretization becomes:![\frac{\phi^{t + 1} - \phi^t}{\Delta t} = \frac{1}{2} \left[ \mathbf{S}(\phi^{t + 1}) + \mathbf{S}(\phi^{t}) \right] \frac{\phi^{t + 1} - \phi^t}{\Delta t} = \frac{1}{2} \left[ \mathbf{S}(\phi^{t + 1}) + \mathbf{S}(\phi^{t}) \right]](/Forums/vbLatex/img/b61c05a828005112b12868aa4d6fc0dc-1.gif) The temporal term is similar to the implicit Euler scheme, and key difference is in semi implicit treatment of the spatial operators. Now, let's assume that an unsteady simulation is performed where the linear system is solved to tight tolerance at each time step before proceeding to next time-step. Thus, equation {Eqn:governingEqn} at any time step 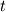 can be approximated as, can be approximated as, 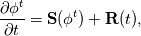 where  is the final residual of the linear system at time-step is the final residual of the linear system at time-step 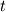 . We can also express the spatial operators in terms of the temporal derivative and the final residual. For example, the equation {Eqn:approxEqn} can be reformulated as . We can also express the spatial operators in terms of the temporal derivative and the final residual. For example, the equation {Eqn:approxEqn} can be reformulated as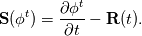 Substituting, 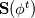 value in the Crank-Nicolson equation {Eqn:implEuler}, we get value in the Crank-Nicolson equation {Eqn:implEuler}, we get![\frac{\phi^{t + 1} - \phi^t}{\Delta t} = \frac{1}{2} \left[ \mathbf{S}(\phi^{t + 1}) + \frac{ \partial{\phi^t}} {\partial t} - \mathbf{R}(t) \right], \frac{\phi^{t + 1} - \phi^t}{\Delta t} = \frac{1}{2} \left[ \mathbf{S}(\phi^{t + 1}) + \frac{ \partial{\phi^t}} {\partial t} - \mathbf{R}(t) \right],](/Forums/vbLatex/img/174dcea904e04b3a7dd8bb98b8d0231f-1.gif) 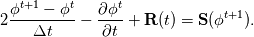 OpenFOAM applies this form of the CrankNicolson scheme with assumption that the linear system residual are driven to machine zero  or atleast insignificantly small. or atleast insignificantly small.Usually in PISO like segregated algorithm, driving the linear system residual to machine zero is very expensive and computationally inefficient. It might be the reason the CrankNicolson scheme is recommended to be used with small blending with implicit Euler scheme. I tested the Crank-Nicolson scheme in a projection algorithm (one outer loop only) where the initial residual are small but higher than PISO type algorithm multiple outer loops. The Crank-Nicolson scheme in the format of equation{Eqn:CNOF} is unstable, but original format (equation {Eqn:CN} is stable. Last edited by rajibroy; May 5, 2020 at 15:35. |
|
|
|

|
|
|
|
|
#11 |
|
Member
Rodrigo
Join Date: Mar 2010
Posts: 98
Rep Power: 16  |
||
|
|

|
|
 |
| Tags |
| crank-nicolson, openfoam, temporal discretization |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| udf error | srihari | FLUENT | 1 | October 31, 2016 15:18 |
| Crank Nicolson scheme | msrinath80 | OpenFOAM Running, Solving & CFD | 6 | November 14, 2010 14:59 |
| Could someone explain the implementation of the convection scheme | liuhuafei | OpenFOAM Running, Solving & CFD | 0 | January 20, 2008 20:18 |
| extrapolation in MUSCL scheme | Chandra | Main CFD Forum | 6 | February 14, 2007 12:21 |
| High order difference scheme for KIVA3v2??? | LiQiang | Main CFD Forum | 1 | May 9, 2005 14:50 |