 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Join Date: Oct 2018
Location: France
Posts: 34
Rep Power: 8  |
Dear Foamers,
I'm trying to implement tables and/or functions for the calculation of state properties in OF6. I adapt the rhoPimpleFoam solver and unfortunately I'm stuck trying to change the temperature calculation as function of enthalpy and pressure. That's my assumption: 1) Using "heRhoThermo" the member function "calculate" in "heRhoThermo.C" calculates the temperature field from solved state variables (the part where the temperature is calculated is colored red). Code:
template<class BasicPsiThermo, class MixtureType>
void Foam::heRhoThermo<BasicPsiThermo, MixtureType>::calculate()
{
const scalarField& hCells = this->he();
const scalarField& pCells = this->p_;
scalarField& TCells = this->T_.primitiveFieldRef();
scalarField& psiCells = this->psi_.primitiveFieldRef();
scalarField& rhoCells = this->rho_.primitiveFieldRef();
scalarField& muCells = this->mu_.primitiveFieldRef();
scalarField& alphaCells = this->alpha_.primitiveFieldRef();
forAll(TCells, celli)
{
const typename MixtureType::thermoType& mixture_ =
this->cellMixture(celli);
TCells[celli] = mixture_.THE
(
hCells[celli],
pCells[celli],
TCells[celli]
);
psiCells[celli] = mixture_.psi(pCells[celli], TCells[celli]);
rhoCells[celli] = mixture_.rho(pCells[celli], TCells[celli]);
muCells[celli] = mixture_.mu(pCells[celli], TCells[celli]);
alphaCells[celli] = mixture_.alphah(pCells[celli], TCells[celli]);
}
volScalarField::Boundary& pBf =
this->p_.boundaryFieldRef();
volScalarField::Boundary& TBf =
this->T_.boundaryFieldRef();
volScalarField::Boundary& psiBf =
this->psi_.boundaryFieldRef();
volScalarField::Boundary& rhoBf =
this->rho_.boundaryFieldRef();
volScalarField::Boundary& heBf =
this->he().boundaryFieldRef();
volScalarField::Boundary& muBf =
this->mu_.boundaryFieldRef();
volScalarField::Boundary& alphaBf =
this->alpha_.boundaryFieldRef();
forAll(this->T_.boundaryField(), patchi)
{
fvPatchScalarField& pp = pBf[patchi];
fvPatchScalarField& pT = TBf[patchi];
fvPatchScalarField& ppsi = psiBf[patchi];
fvPatchScalarField& prho = rhoBf[patchi];
fvPatchScalarField& phe = heBf[patchi];
fvPatchScalarField& pmu = muBf[patchi];
fvPatchScalarField& palpha = alphaBf[patchi];
if (pT.fixesValue())
{
forAll(pT, facei)
{
const typename MixtureType::thermoType& mixture_ =
this->patchFaceMixture(patchi, facei);
phe[facei] = mixture_.HE(pp[facei], pT[facei]);
ppsi[facei] = mixture_.psi(pp[facei], pT[facei]);
prho[facei] = mixture_.rho(pp[facei], pT[facei]);
pmu[facei] = mixture_.mu(pp[facei], pT[facei]);
palpha[facei] = mixture_.alphah(pp[facei], pT[facei]);
}
}
else
{
forAll(pT, facei)
{
const typename MixtureType::thermoType& mixture_ =
this->patchFaceMixture(patchi, facei);
pT[facei] = mixture_.THE(phe[facei], pp[facei], pT[facei]);
ppsi[facei] = mixture_.psi(pp[facei], pT[facei]);
prho[facei] = mixture_.rho(pp[facei], pT[facei]);
pmu[facei] = mixture_.mu(pp[facei], pT[facei]);
palpha[facei] = mixture_.alphah(pp[facei], pT[facei]);
}
}
}
}
Code:
scalar THE
(
const Thermo& thermo,
const scalar h,
const scalar p,
const scalar T0
) const
{
return thermo.THa(h, p, T0);
}
Code:
template<class Thermo, template<class> class Type> inline Foam::scalar Foam::species::thermo<Thermo, Type>::THa ( const scalar ha, const scalar p, const scalar T0 ) const { return T ( ha, p, T0, &thermo<Thermo, Type>::Ha, &thermo<Thermo, Type>::Cp, &thermo<Thermo, Type>::limit ); } But until now I couldn't find the piece of code calculating the temperature field from the given input variables. Does anybody know, where to find that or am I on the wrong track? Thanks in advance and have a nice evening (or whatever), stockzahn |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Aug 2015
Posts: 494
Rep Power: 15  |
||
|
|

|
|
|
|
|
#3 | |
|
Member
Join Date: Oct 2018
Location: France
Posts: 34
Rep Power: 8  |
Quote:
Dear Caelan, thank you very much for this link - the information indeed was very helpful and (I think) I was able to follow almost all the steps how the enthalpy/internal energy field is created and, after solving the LES, the temperature is obtained from the resulting field. However, unfortunately I have a missing link I couldn't find and maybe you or somebody else know where to find it. Examplarily I use the rhoPimpleFoam solver to explain my problem: In the file createFields.H the object thermo of the class fluidThermo is created. Code:
autoPtr<fluidThermo> pThermo ( fluidThermo::New(mesh) ); fluidThermo& thermo = pThermo(); Code:
virtual tmp<volScalarField> he ( const volScalarField& p, const volScalarField& T ) const = 0; Code:
template<class BasicThermo, class MixtureType> class heThermo : public BasicThermo, public MixtureType { ... virtual tmp<volScalarField> he ( const volScalarField& p, const volScalarField& T ) const; ... } Code:
volScalarField& he = thermo.he(); stockzahn |
||
|
|

|
||
|
|
|
#4 |
|
New Member
Russian Federation
Join Date: Apr 2020
Posts: 18
Rep Power: 6  |
Hello,
I am concerned with the same problem, but the link provided above does not work. Could you explain how the temperature is obtained from the resulting field if you understand it? The meaning of "he" is more intricated for me be because of diffusivity term in the EEq.H of buoyantPimpleFoam. In the simplest case the energy equation in the buoyantPimpleFoam can simplified as Code:
fvm::ddt(rho, he)
+ fvm::div(phi, he)
- fvm::laplacian(alpha, he)
==
+ fvOptions(rho, he)
Code:
fvm::laplacian(alpha, he) Regards |
|
|
|

|
|
|
|
|
#5 |
|
Member
Join Date: Oct 2018
Location: France
Posts: 34
Rep Power: 8  |
Dear fetc95,
I currently dealt with exactly the same question. Unfortunately I wasn't able to find an answer I'm sure about, so I only can tell you my thoughts. Maybe you can verify or falsify them. - The diffusion term normally should be fvc::laplacian(kappa, T) - The disadvantage is that the diffusion cannot be calculated implicitly - The term fvm::laplacian(alpha, he) works if the enthalpy/internal energy is proportional to the temperature; only the factor Cp^-1/Cv^-1 (specific heat capacity), which is contained in alpha, must be taken into account (in OF alpha = kappa/Cp) - This works for simple models, e.g. perfect gas - In my case I integrated a property library (of helium); at some states helium has an inverse correlation between temperature and enthalpy/internal energy, therefore I think I must not use the implicit term, but have to use fvc::laplacian(kappa, T) which increase instability To sum up: In my understanding the implicit term fvm::laplacian(alpha, he) can be used, when 1) T proportional to he 2) Cp * T = h | Cv * T = e otherwise the code has to be changed to calculate the diffusion explicitly from fvc::laplacian(kappa, T) What do you think? |
|
|
|

|
|
|
|
|
#6 | |
|
New Member
Russian Federation
Join Date: Apr 2020
Posts: 18
Rep Power: 6  |
Quote:
I thought about this issue yesterday and today and that what I think. It means that all compressible, combustion, heat transfer, etc. solvers are not valid for cases of temperature-dependent heat capacity and are valid only when hConst or eConst is choosen. I believe such important fact would be mentioned somewhere in openfoam if it was so. I also found the following in CFD direct https://cfd.direct/openfoam/energy-equation/. I did not find there any information about requirement of proportionality between 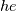 and and 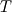 . .I suggest the following. Let us want to solve some heat equation with temperature-dependent heat capacity, e.g., hPolynomial. So in LHS of this equation we have a term  If we want to solve it in conservative form we can reformulate it by locating c\left(T\right) under derivative as follows 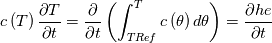 Similarly we can do when formulating the heat flux law 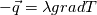 by multiplying and dividing it by  and locating and locating  under grad: under grad: Check me am I right mathematically. So, I suggest that there is no requirement of proportionality between 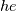 and and 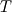 , and the only requirement is the proportionality between , and the only requirement is the proportionality between  and and 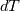 . Thus, the above formulation of the heat equation is valid for cases of temperature-dependent heat capacity. This is to be valid for any function c(T) which satisfies the following: . Thus, the above formulation of the heat equation is valid for cases of temperature-dependent heat capacity. This is to be valid for any function c(T) which satisfies the following:1) Finite number of points of jump discontinuities in range [TRef,TMax] 2) No essential discontinuities in range [TRef,TMax] Another question is that how the temperature is calculated in case of non-constant heat capacity. E.g. if the c(T) is a polynomial of some order n  he is a polynomial of n+1 order  The above algebraic polynomial equation is to be solved for temperature for all x, y, z and t. The advantage of this equation is that we know that for T>0 the he as function of T is always monotonical. It means that for fixed x, y, z and t it has only one solution. It seems that there is some iteration procedure is needed in OpenFOAM to obtain the temperature. It would be good to find it in the code. Last edited by fetc95; April 21, 2020 at 00:41. Reason: extra symbols |
||
|
|

|
||
|
|
|
#7 | |
|
Member
Join Date: Oct 2018
Location: France
Posts: 34
Rep Power: 8  |
First of all thanks for this discussion. I also would like to start with the plausibility check:
Quote:
On the other hand, the idea to treat the diffusion term implicitly to increase stability seems so obvious that I would be surprised, if I wouldn't have read it in a book until now - but actually I haven't. Maybe I've got the wrong books ... Regarding the math, just to be sure about the last line: Locating the specific heat capacity inside the gradient only is allowed, if it is not a function of a spatial coordinate (so c != f(x,y,z)), so if it is constant. Or am I wrong? But for the discretized equation we can use (different) constant values for each cell, therefore I would agree using discrete values. Then the temperature gradient only would be multiplied by certain factor, which is "corrected" by using alpha instead of kappa. Considering it like that, it maybe could work anyway for discretized functions, independent of the model to calculate the specific property. But for sure the code would be helpful, since normally in the discretized diffusion term the face values of the diffusive parameter are used, which would lead to a (small) error, if theay are corrected by the cell value of the diffusive parameter (alpha in this case). E.g. for 1D: ![D = \frac{\Delta t}{\Delta x^2 c_C} \left[\kappa_w c_w T_W - \left(\kappa_w c_w + \kappa_e c_e \right) T_C + \kappa_e c_e T_E \right] D = \frac{\Delta t}{\Delta x^2 c_C} \left[\kappa_w c_w T_W - \left(\kappa_w c_w + \kappa_e c_e \right) T_C + \kappa_e c_e T_E \right]](/Forums/vbLatex/img/9f0612cb4306f304af83a02f2d3571b2-1.gif) Still, somehow for me this only works if he is more or less an "image" of the temperature - multiplied by a factor c. I have to admit that until now I tried to find the code for "laplacian" a few times, but there are many different files and for me the structure of this basic files functions is not clear yet, so I never spent the time to dig into it until now - although I now that sooner or later that will be necessar anyway ... What do you think? And thanks again for starting this discussion stockzahn |
||
|
|

|
||
|
|
|
#8 | |
|
New Member
Russian Federation
Join Date: Apr 2020
Posts: 18
Rep Power: 6  |
Hello,
I am also grateful that you participate this discussion. I firstly qoute this: Quote:
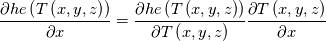 The specific heat capacity in our case is temperature derivative of "he". For example see the paper 10.1016/j.applthermaleng.2009.04.018 figures 1 and 2. The blue line is internal energy, the black line is specific heat capacity. You can see that the black line is derivative of the blue line. So, on the contrast, you can back locate this term under derivative. Note that when I located the specific heat capacity under grad I located not directly heat capacity but its integral over temperature. In the simplest case of constant specific heat capacity this integral equals just c*T. I think we must to find code of obtaining temperature from "he". If that code is constructed for c(T), not only constant, it is obviously that this heat equation is valid for any function c(T). But while we will look for the code I offer to turn back to your concrete case to which the current thread is devoted. Did I understand you correctly that when you implemented fvm::laplacian(alpha, he) you obtained the unexpected results and when you implemented fvc::laplacian(kappa,T) you obtained the results you are expected but the stability decreased? |
||
|
|

|
||
|
|
|
#9 | ||||
|
Member
Join Date: Oct 2018
Location: France
Posts: 34
Rep Power: 8  |
Quote:
Quote:
Quote:
I'm not sure if I will be able to start looking for the laplacian code before the weekend, but maybe I will try it then. Quote:
stockzahn |
|||||
|
|

|
|||||
|
|
|
#10 |
|
New Member
Russian Federation
Join Date: Apr 2020
Posts: 18
Rep Power: 6  |
Dear stockzahn
Could you hint me what procedure do you use in your solver to get the temperature for using it in the equation? |
|
|
|

|
|
|
|
|
#11 | |
|
Member
Join Date: Oct 2018
Location: France
Posts: 34
Rep Power: 8  |
Quote:
Dear fetc95, when I made my first thermodynamical model, I tried to write down some procedures and explanations - unfortunately the document still contains some typos. However, in the end there are some graphics showing the calling paths for getting the properties. Does that answer your question? Otherwise please let me know which temperature at which point of the calculation you are interested in. Maybe I have an idea... thermophysicalModel_small.pdf sincerely, stockzahn |
||
|
|

|
||
|
|
|
#12 | |
|
New Member
Russian Federation
Join Date: Apr 2020
Posts: 18
Rep Power: 6  |
Quote:
About your ideas which you tell earlier. I look at the of function T in thermoI.H. As i tell it is iteration procedure for obtaining temperature from some function F(T, p) which depends on case. Concretely it is the Newton method, which usually has good convergence rate so the temperature calculation has not be expencive. When we consider the term laplacian(kappa/c(T), he(T)) we do not need any special implementation of the laplacian(*,*) for this case because if we consider this term on some time/iteration step (n+1), we consider the first argument of the function on step n. So from the point of view of (n+1) th step it is just a known volume field. All we need is to interpolate it on the cell faces. |
||
|
|

|
||
|
|
|
#13 | |||
|
Member
Join Date: Oct 2018
Location: France
Posts: 34
Rep Power: 8  |
Quote:
Quote:
I don't even use this function, since I retrieve my temperature values from a library function (T = f(p,h)). But just if I understand the code correctly: The function T in thermoI.H varies the temperature until it results in the correct enthalpy value (for a fixed pressure)? If I try to "translate" this line: I get (ignoring the limit)  That again, if I understand correctly, can only work if  , or what am I missing? Unless c_p is just used as a mathematical factor without a physical meaning ... , or what am I missing? Unless c_p is just used as a mathematical factor without a physical meaning ...Quote:
Still we use the enthalpy gradient instead of the temperature gradient. Can we use it, since in the small temperature range of a cell and its neighbours we can assume the specific heat capacity more or less constant? We do not need the absolute temperature, just the difference, therefore it doesn't really matter what the value of c is. But we'll get an error which increases with increasing variation of c with changing T. In your previous posts you pointed out, that the approach would work if the enthalpy would be calculated as integral of c(T)dT. But I can't find any function doing that. |
||||
|
|

|
||||
|
|
|
#14 | |
|
New Member
Russian Federation
Join Date: Apr 2020
Posts: 18
Rep Power: 6  |
Hello!
Quote:
Let's try to gather information from your first post with your previous posts. As you rote the temperature is calculated Code:
forAll(TCells, celli)
{
const typename MixtureType::thermoType& mixture_ =
this->cellMixture(celli);
TCells[celli] = mixture_.THE
(
hCells[celli],
pCells[celli],
TCells[celli]
);
psiCells[celli] = mixture_.psi(pCells[celli], TCells[celli]);
rhoCells[celli] = mixture_.rho(pCells[celli], TCells[celli]);
muCells[celli] = mixture_.mu(pCells[celli], TCells[celli]);
alphaCells[celli] = mixture_.alphah(pCells[celli], TCells[celli]);
}
Code:
scalar THE
(
const Thermo& thermo,
const scalar h,
const scalar p,
const scalar T0
) const
{
return thermo."FUNCTION"(h, p, T0);
}
Code:
template<class Thermo, template<class> class Type>
inline Foam::scalar Foam::species::thermo<Thermo, Type>::THa
(
const scalar ha,
const scalar p,
const scalar T0
) const
{
 using the Newton method:  If we gather all of this we see that to calculate temperature we go through all cell and for every cell we call the function: 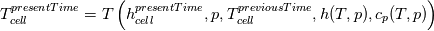 Since in the 5th argument of the function T() is as said in the description a derivative of the 4th argument, we see that cp is passed as derivative of h. And it does not depend on that cp is constant or not. We already due to this can believe that  and correspondingly 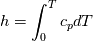 Now let's try to talk about integration of cp. We do not find an implementation of this integration in general case because it would be very costly numerically. So the integration is to depend on concrete chosen model hConst, hPolynimial, etc. For example when cp is constant this integral is 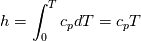 and you can find in hConstThermol.H in line 109 that h is calculated as cp times T. Now let's consider the case of hPolynomial when cp is polynomial. In this case is 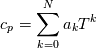 The integration of this gives  Since we know that enthalpy or internal energy equals zero at zero temperature we set b=0. So, summarizing we can say that in implementation to set the polynomial we just need to store the order of the polynomial and array of its coefficients. Suppose we have an array V of size M=N+1 of polynomial coefficients, where ![V[j] = a_j V[j] = a_j](/Forums/vbLatex/img/9e2e65e463cf4fd0ec5e3060227ea662-1.gif) Such information we obtain from thermoPhysicalProperties when setting the cp-polynomial coefficients. So now all we need to set the integral of cp is set an array newV of size M+1 where Code:
newV[0] = 0; newV[j+1] = V[j]/(j+1), where j = 0,1, …, M Code:
hCoeffs = cpCpoeffs.integral(). We could check my suggestion by solving the following model problem. Consider the equation:  This equation can be reformulated as  Setting the boundary condition this equation can be easily solved with finite-different method which is easy to implement. From the other hand this equation can be solved with thermoFoam. If my suggestion is right these solutions must concise. |
||
|
|

|
||
|
|
|
#15 |
|
Member
Join Date: Oct 2018
Location: France
Posts: 34
Rep Power: 8  |
First of all: Sorry for the late reply - it was a strange week. Plus I obviously need much more time to process this mathematically. You are really good at this - I'm impressed. Thanks to your last post I think I've achieved a better understanding and thanks to your formulation I finally get how the calculation of
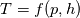 works. works.If I get it right, for the polynomial approach, the calculation of the polynomial coefficents for the enthalpy is implemented based on the polynoms of the specific heat capacity. I assume similar pieces of code exist for the other models. Let's have a look at the calling path to the function T in thermoI.H (using the Newton method): Code:
template<class Thermo, template<class> class Type>
inline Foam::scalar Foam::species::thermo<Thermo, Type>::T
(
scalar f,
scalar p,
scalar T0,
scalar (thermo<Thermo, Type>::*F)(const scalar, const scalar) const,
scalar (thermo<Thermo, Type>::*dFdT)(const scalar, const scalar)
const,
scalar (thermo<Thermo, Type>::*limit)(const scalar) const
) const
{
if (T0 < 0)
{
FatalErrorInFunction
<< "Negative initial temperature T0: " << T0
<< abort(FatalError);
}
scalar Test = T0;
scalar Tnew = T0;
scalar Ttol = T0*tol_;
int iter = 0;
do
{
Test = Tnew;
Tnew =
(this->*limit)
(Test - ((this->*F)(p, Test) - f)/(this->*dFdT)(p, Test));
if (iter++ > maxIter_)
{
FatalErrorInFunction
<< "Maximum number of iterations exceeded: " << maxIter_
<< abort(FatalError);
}
} while (mag(Tnew - Test) > Ttol);
return Tnew;
}
Code:
template<class Thermo, template<class> class Type>
inline Foam::scalar Foam::species::thermo<Thermo, Type>::THa
(
const scalar ha,
const scalar p,
const scalar T0
) const
{
return T
(
ha,
p,
T0,
&thermo<Thermo, Type>::Ha,
&thermo<Thermo, Type>::Cp,
&thermo<Thermo, Type>::limit
);
}
Code:
template<class EquationOfState, int PolySize>
inline Foam::scalar Foam::hPolynomialThermo<EquationOfState, PolySize>::Cp
(
const scalar p, const scalar T
) const
{
return CpCoeffs_.value(T) + EquationOfState::Cp(p, T);
}
Code:
template<class Specie>
inline Foam::scalar Foam::rPolynomial<Specie>::Cp(scalar p, scalar T) const
{
return 0;
}
Code:
fvm::laplacian(turbulence->alphaEff(), he) Code:
template<class EquationOfState, int PolySize>
inline Foam::scalar Foam::hPolynomialThermo<EquationOfState, PolySize>::Ha
(
const scalar p, const scalar T
) const
{
return hCoeffs_.value(T) + EquationOfState::H(p, T);
}
Code:
hCoeffs_ Code:
cpCoeffs_ For the 1D-case the (explicit) FDM discretization of your last two equations (for  ) should be ) should be    Using just "values" of the diffusion coefficients, the equations for temperature and enthalpy are identical they differ only by the source terms at the boundaries. That works if we assume the difference of the specific heat capacities for two neighboured cells negligible. Or did you have in mind something else? |
|
|
|

|
|
|
|
|
#16 | ||
|
New Member
Russian Federation
Join Date: Apr 2020
Posts: 18
Rep Power: 6  |
Hi, stockzahn
I start the reply from the end. Quote:
I also cannot understand why you retrieve cp from derivative in equation for h. I will consider the case of temperature dependent cp. Let's for example  The h in this case is  So the equation is (let 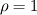 ) )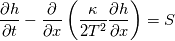 The boundary conditions for this equation can be calculated using the conditions for temperature and the dependencies between h, cp and T. Let in the following ![x \in \left[ 0,1 \right],
\left.T\right|_{x=0} = T_0,
\left.\frac{\partial T}{\partial x}\right|_{x=1} = 0 x \in \left[ 0,1 \right],
\left.T\right|_{x=0} = T_0,
\left.\frac{\partial T}{\partial x}\right|_{x=1} = 0](/Forums/vbLatex/img/2249792f200b1485c4a4cf05a97ffb15-1.gif) The condition for the function h at x=0 you can directly calculate from known function h = h(T):  The gradient condition at x = 1 can be obtained by multiplying and dividing it by cp and doing the same procedure as I used several posts above: 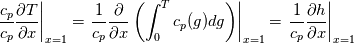 Finally  In OF or in implicit FVM we will actually solve the following equation on every moment of time:  with conditions:  where 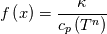 f(x) is calculated from temperature obtained on the previous time step and on the current step represents just a known field. It seems some decoupling, but it can be compensated by doing several iterations on every time step as it is in OF. And there is know need to assume the difference of the specific heat capacities for two neighboured cells negligible. You just need to solve the Poison equation on every step with coordinate-dependent diffusion coefficient. Quote:
Code:
cpCoeffs_.value(T) Quote:
|
|||
|
|

|
|||
|
|
|
#17 | |
|
Member
Join Date: Oct 2018
Location: France
Posts: 34
Rep Power: 8  |
Quote:
Code:
fvm::laplacian(turbulence->alphaEff(), he) Code:
volScalarField& he = thermo.he(); Code:
virtual volScalarField& he()
{
return he_;
}
turbulence->alphaEff() is a function in the turbulence class, which calls the function alphaEff(alphat) in heThermo.C: Code:
template<class BasicThermo, class MixtureType>
Foam::tmp<Foam::volScalarField>
Foam::heThermo<BasicThermo, MixtureType>::alphaEff
(
const volScalarField& alphat
) const
{
tmp<Foam::volScalarField> alphaEff(this->CpByCpv()*(this->alpha_ + alphat));
alphaEff.ref().rename("alphaEff");
return alphaEff;
}
So I cannot see, where a function is used, for me it seems that (constant) values are passed to the solver. So I'm not saying it is not possible to set up a FDM simulation with cp = f(T) - of course we can. I don't get how OF does it and as I just tried to explain: What I can see from the code an according small FDM simulation would be run with a temperature dependent specific heat capacity, but not passing the function, just the value:   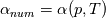  But maybe I have to dig a little bit deeper and calling paths contain more steps than I think right now. Last edited by stockzahn; May 5, 2020 at 14:50. |
||
|
|

|
||
|
|
|
#18 |
|
New Member
Russian Federation
Join Date: Apr 2020
Posts: 18
Rep Power: 6  |
Unfortunately, I cannot understand where you see that the properties passed to the solvers must be constant. In what part of the code do you see that the field which is passed as diffusion property (the 1th argument of the laplacian) cannot be varied from cell to cell? The alpha (or alphaEff, it is not important) is a volScalarField as you say. But you also say "with no any information". The type vol<Type>Field already means that this property can be varied from cell to cell. On the current solution step this field is already known and can be used in matrix coefficients of the linear equation system which is solved for defining the sought field. What also information is needed? May be it is needed to find how the diffusion coefficient alpha is calculated.
In OpenFOAM descriptions, e.g., in Extended Code Guide in openfoam.com or in Programmers Guide from openfoam.org the term Code:
laplacian(Gamma, G)  or more exactly 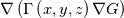 so the diffusion coefficient in general can be the function of coordinates, i.e., volField or surfaceField and the passed properties must not be constant. In addition, I am sure that there is no point for the developers to implement the diffusion term only for constant diffusion coefficient. Anyway, I believe that if it was so it would be mentioned in the programmers guide. But if you are doubt we need to analyze the code of fvm::laplacian operator in similarity with that we done for thermo models. However, I think that it is obviously. Concretely, I am sure that after the Gauss integration over the finite volume of the above term and discretization of the surface gradients in 1D case the OF gets: 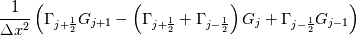 and not  From the information provided by you I cannot see that there is some contradiction and that it is impossible. The implementation of the first way of discretization is not programmatically expensive, so I do not think that OF developers ignored that. Your second scheme is to be like this  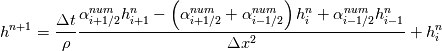 where 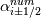 are values of field are values of field  interpolated onto cell faces. Here is no any need to know how the interpolated onto cell faces. Here is no any need to know how the  was calculated. All we need is to know the cell values of the field was calculated. All we need is to know the cell values of the field  which were obtained when thermo.correct() was called on the previous step. The Laplacian(alpha,h) just will take this known field and calculate the diffusion term. which were obtained when thermo.correct() was called on the previous step. The Laplacian(alpha,h) just will take this known field and calculate the diffusion term.
Last edited by fetc95; May 5, 2020 at 20:52. Reason: adding |
|
|
|

|
|
|
|
|
#19 |
|
Member
Join Date: Oct 2018
Location: France
Posts: 34
Rep Power: 8  |
[QUOTE=fetc95;768930]
Unfortunately, I cannot understand where you see that the properties passed to the solvers must be constant. [QUOTE/] I don't know why I can't express my self adequately. I didn't mean that the entire field has the same value, but the single values of the cells (which of course can differ) are passed as numerical value not as functions. But I see that you can think that, since I wrote the equation in my last post as I did (and not like in my (overall) post #7). I try to be more precise. I try again: If values are passed and not functions then 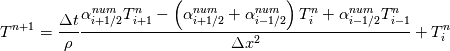 corresponds to 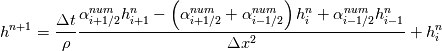 which only works, if  or or 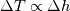 and that's only valid, if the change of and that's only valid, if the change of 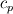 over the temperature range over the temperature range  - -  including including  is negligible. Else the enthalpy (evolution) does not represent the temperature (evolution). is negligible. Else the enthalpy (evolution) does not represent the temperature (evolution).
|
|
|
|

|
|
|
|
|
#20 |
|
New Member
Russian Federation
Join Date: Apr 2020
Posts: 18
Rep Power: 6  |
[QUOTE=stockzahn;769086]
Quote:
It seems that you ignore some moments we already discussed above. The first scheme in your last post is valid only when cp = const, i.e., it is equivalent to (for non-constant kappa)  while the second scheme is valid for any variable cp. So, I cannot understand what you mean when you say that your two schemes "correspond" to each other. The first scheme does not correspond to the second one. You are right that your first scheme in your last post works only when cp=const. But it is not right for the second scheme, because it works for any cp. Let us try again. You have an equation (rho = 1) 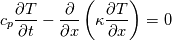 Let us in the following believe that cp and kappa depend on T  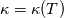 This equation you also can write as follows  Now we use that the changing of enthalpy is proportional to the changing of the temperature  which gives  which gives 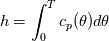 For constant cp:  For polynomial cp: 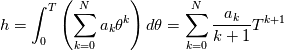 and for any function cp(T) which can be analytically integrated over T you can obtain the analytical expression for h=h(T). As I wrote above you can use the following transformations 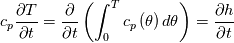  Substituting these in the original equation we get the fully mathematically equivalent equation  where  The only difference between this equation and the first equation is that the last is written in "conservative" form while the first one does not. The first equation is conservative only when cp=const. In other issues these equations are equivalent. The procedure of the numerical solving of the first equation (in temperature terms) is as follows: Suppose you calculated the temperature on some step n which is T^n. Now in the end of the nth step you calculate: 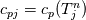 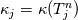 After this you can pass them to the (n+1) step and calculate the temperature T^(n+1)  Note that our numerical method does not know and does not remember that cp_j and kappa_j were calculated as functions of temperature on the previous step. On the step (n+1) it senses them just as some known grid fields in FDM or volume fields in FVM. In other words the last scheme will not be changed if you will calculate cp_j and kappa_j on the previous step in some other way. On what step of this procedure do you need to pass them as "functions"? You just calculate this volume fields on previous step in some given way (in the present case - as functions of temperature, but it is not essential) and then pass them to the following step. Similarly it is when you solve the equivalent equation for the enthalpy h. You calculated the temperature on some step n which is T^n. Now in the end of the nth step you calculate: 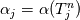 After this you can pass alpha to the (n+1) step and calculate the enthalpy h^(n+1) 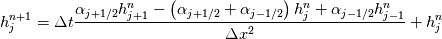 After this you calculate the temperature T^(n+1) solving the equation:  for every j using the Newton method as we discussed above. Similarly, we see that our method does not know and does not remember that alpha_j was calculated as function of temperature. And it does not need to know that. On the step (n+1) it senses alpha just as some known volume field. You just calculate this volume field on previous step in some given way and then pass it to the following step. This works for any function h=h(T) and cp=cp(T) and there is no need of  . The only need is . The only need is 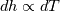 . However, you should not intricate these two relations. These are different relations. The first one is an algebraic relation. The second one is a differential relation . However, you should not intricate these two relations. These are different relations. The first one is an algebraic relation. The second one is a differential relation
Last edited by fetc95; May 7, 2020 at 21:15. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| efficiency calculation using reference temperature | lostking18 | CFX | 0 | September 10, 2019 14:08 |
| Warning...Extrapolating on the temperature calculation | -nan | CONVERGE | 7 | April 21, 2017 12:10 |
| Dynamic mesh adaption in parallel calculation | xh110120 | FLUENT | 1 | March 12, 2016 09:05 |
| where is the calculation of the temperature field | Tobi | OpenFOAM | 1 | July 30, 2012 11:40 |
| temperature / enthalpy fields depending on type of fvPatchField | astein | OpenFOAM Programming & Development | 0 | June 28, 2010 08:10 |