 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
K
Join Date: Mar 2018
Posts: 34
Rep Power: 8  |
Hey everyone
I was trying to implement Laplace-Beltrami operator of velocity 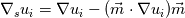 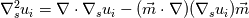 So this is what I tried volVectorField GradUi= fvc::grad(phi) - (m & fvc::grad(phi))*m; volScalarField LBUi= fvc::div(GradUi) - (m & fvc::grad( GradUi & m ); But the problem with is implementation is that GradUi (a tensor) fvc::div(GradUi) is a vector because divergence of tensor (m & fvc::grad( GradUi & m ) is a scalar Can some one help with implementing these equation? Thanks in advance 
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Andrew Somorjai
Join Date: May 2013
Posts: 175
Rep Power: 13  |
Quote:
Last edited by massive_turbulence; February 21, 2019 at 05:45. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Andrew Somorjai
Join Date: May 2013
Posts: 175
Rep Power: 13  |
Quote:
There maybe a way to represent the solution of a scalar and vector commutative operation as a parametric scalar equation but as far as I can see openfoam doesn't have such a representation. You would have to overload the minus operator for your equation to take the scalar and vector types and then create a new type that takes the components of each scalar and vector as a parametric equation. |
|
|
|

|
|
|
|
|
#4 |
|
Member
K
Join Date: Mar 2018
Posts: 34
Rep Power: 8  |
I looked around a little bit and as far I can see the equation what I have wrote before is what people have used.
I found this implementation to atleast compile: surfaceVectorField GradUi= fvc::interpolate(fvc::grad(phi)) - (m & fvc::interpolate(fvc::grad(phi)) )*m; surfaceScalarField LBUi1= fvc::interpolate(fvc::div(GradUi)) & mesh.Sf(); surfaceScalarField LBUi2= (m & ( fvc::interpolate(fvc::grad(GradUi)) ) ) & m; LBUi = (LBUi1+LBUi2)/mesh.magSf(); I used the normal surface vector to the cell (mesh.Sf()) to ensure that the terms are compatible. I found a similar approach while calculating the curvature of interface where curvature which is defined as 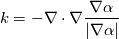 and implemented as surfaceVectorField nHatfv(gradAlphaf/(mag(gradAlphaf) + deltaN)); surfaceScalarField nHatf = nHatfv & Sf; volScalarField K = -fvc::div(nHatf); What do you think of the the way I implemented it? |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Andrew Somorjai
Join Date: May 2013
Posts: 175
Rep Power: 13  |
Quote:
It's nice! |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| ANSYS Workbench on "Uncertified" Linux Distros | hsr | CFX | 289 | April 20, 2023 10:23 |
| FLUENT installation on UBUNTU 12.04 (LTS) | teymourj | FLUENT | 2 | March 1, 2017 23:24 |
| Cahn Hilliard implementation (Biharmonic operator) | jdpeterson3 | OpenFOAM Running, Solving & CFD | 0 | February 15, 2016 03:36 |
| Implementation issues of fvSchemes / laplacianScheme, in particular gaussLaplacianSch | thomek | OpenFOAM Programming & Development | 0 | October 18, 2010 06:10 |
| Laplace operator in finite element formulation | Rafael | Main CFD Forum | 2 | October 19, 2004 22:09 |