 |
|
|
[Sponsors] | |||||
adding viscous dissipation to openfoam solver |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
A. Min
Join Date: Mar 2015
Posts: 308
Rep Power: 12  |
Hi
I want to add viscous dissipation to energy eqn. but my fluid is not Newtonian and has a special stress tensor. So the work of stress tensor field is "tau && grad(U)" 1- is it a correct relation for work of stress tensor field? or I should write: tau && [grad(U) + transpose of (grad(U))] 2- is it correct to write: solve ( fvm::div(phi, T) - fvm::laplacian(alphaEff, T) - tau && grad(U) ); thank you |
|
|
|

|
|
|
|
|
#2 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Hi,
I would expect to have the shear heating given as:  However, I am not sure about Non-Newtonian fluids. The only change should be in the viscosity (which does not follow a linear profile). The stress tensor itself should be similar to those of Newtonian fluids. I might be wrong in that case and have to proof it somewhere in literature. The equation of the shear-heating is correct.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
A. Min
Join Date: Mar 2015
Posts: 308
Rep Power: 12  |
Quote:
tau && [grad(U) + transpose of (grad(U))] this relation is valid for viscoelastic fluid, just we should use viscoelastic stress tensor. 
|
|
|
|

|
|
|
|
|
#4 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Thanks for the reply. Can you give me a reference for proof? Thus, I can add this information to my book.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Join Date: Mar 2014
Location: Czech Republic
Posts: 29
Rep Power: 14  |
Hi,
this is incorrect. If Tau is Cauchy stress tensor then (does not matter what kind, i.e., viscoelastic fluid etc.)  but note that by "additing" transpose of gradient of the velocity to the formula, you really gives less information in the formula as  is symmetric part of the gradient of the velocity. This is indeed used in many proofs. Best Ondra |
|
|
|

|
|
|
|
|
#6 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
I don't get your point. Who is wrong and what is correct now?
In general the Cauchy stress tensor is defined as  while the shear tensor is while the shear tensor is  such as: such as: while  is the deviatoric part of the Cauchy stress tensor and the negative pressure represents the hydrostatic part such as: is the deviatoric part of the Cauchy stress tensor and the negative pressure represents the hydrostatic part such as: Based on Bird et al. the viscose heating is related to:  but it is mentioned that you have to have an symmetric shear tensor (  ). Thus, your relation is only valid for symmetric ones; if this was the thing you wanted to point out, I just clearyfied the things. If there is some mistake, please don't hesitate to correct me. ). Thus, your relation is only valid for symmetric ones; if this was the thing you wanted to point out, I just clearyfied the things. If there is some mistake, please don't hesitate to correct me.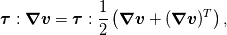 only valid for symmetric shear rate tensor only valid for symmetric shear rate tensor  while  is given as: is given as:![\textbf{D} = \frac{1}{2} [\nabla \otimes \textbf{U} + (\nabla \otimes \textbf{U})^\mathrm{T}] \textbf{D} = \frac{1}{2} [\nabla \otimes \textbf{U} + (\nabla \otimes \textbf{U})^\mathrm{T}]](/Forums/vbLatex/img/1d10e2af775eaebfd24f635cb56e2cea-1.gif)
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#7 |
|
New Member
Join Date: Mar 2014
Location: Czech Republic
Posts: 29
Rep Power: 14  |
Quote:
Sorry, I forget to cite alimea post. My post was reaction mainly to point-out that it does not matter if the Newtonian fluid is under consideration. I defined Cauchy stress as Tau not Sigma, but it really does not matter in our discussion. Cauchy stress is always symmetric and the D is defined as symmetric part of the gradient of the velocity. So the formula holds always within classical mechanics of continuum. |
|
|
|

|
|
|
|
|
#8 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
I agree, the nomenclature does not play a big deal here. However, do you have any example in which the Cauchy stress tensor, or the general formulation - given in Gurtin et al. - The Mechanics and Thermodynamics of Continua - is not symmetric?
PS: Did you comment in the quotes? I did not mean the gradient. What did you mean there?
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#9 |
|
New Member
Join Date: Mar 2014
Location: Czech Republic
Posts: 29
Rep Power: 14  |
No, as long as conservation of angular momentum holds the Cauchy stress tensor is symmetric.
|
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Hojatollah Gholami
Join Date: Jan 2019
Posts: 171
Rep Power: 7  |
Dear alimea
Do you add viscous dissipation to energy equation? I have the same problem, if favor me, I pleasure. thanks |
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
A. Min
Join Date: Mar 2015
Posts: 308
Rep Power: 12  |
||
|
|

|
|
|
|
|
#12 |
|
Senior Member
Hojatollah Gholami
Join Date: Jan 2019
Posts: 171
Rep Power: 7  |
Dear alimea
I want to add a viscous heating term to energy equation as below 
|
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
A. Min
Join Date: Mar 2015
Posts: 308
Rep Power: 12  |
||
|
|

|
|
|
|
|
#14 | |
|
Senior Member
Hojatollah Gholami
Join Date: Jan 2019
Posts: 171
Rep Power: 7  |
I want to add last term to energy equation, So I uses
Quote:
|
||
|
|

|
||
|
|
|
#15 |
|
Senior Member
A. Min
Join Date: Mar 2015
Posts: 308
Rep Power: 12  |
||
|
|

|
|
|
|
|
#16 |
|
Senior Member
Hojatollah Gholami
Join Date: Jan 2019
Posts: 171
Rep Power: 7  |
||
|
|

|
|
|
|
|
#17 | |
|
Senior Member
|
Quote:
Code:
// Step 1: Calculate deviatoric stress tensor
volSymmTensorField devRhoReff = turbulence->devRhoReff();
// Step 2: Compute the velocity gradient tensor
volTensorField gradU = fvc::grad(U);
// Step 3: Compute the viscous dissipation term
volScalarField viscousDissipation("viscousDissipation", devRhoReff && gradU);
// Optional: Log the min and max of viscous dissipation for debugging
Info << "Viscous Dissipation (min, max): "
<< min(viscousDissipation).value() << ", "
<< max(viscousDissipation).value() << endl;
// Step 4: Construct the enthalpy equation
fvScalarMatrix hEqn
(
fvm::ddt(rho, h)
+ fvm::div(phi, h)
- fvm::laplacian(turbulence->alphaEff(), h)
==
DpDt + viscousDissipation
);
https://develop.openfoam.com/Develop...sDissipation.C |
||
|
|

|
||
 |
| Tags |
| openfoam, viscous dissipation |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| PEMFC model with FLUENT | brahimchoice | FLUENT | 22 | April 19, 2020 16:44 |
| Density-based, fully-coupled, compressible solver in OpenFOAM? | francesco_capuano | OpenFOAM Running, Solving & CFD | 7 | November 20, 2018 14:12 |
| Parallelisation of a new solid solver in OpenFOAM | Jibran | OpenFOAM Programming & Development | 3 | August 25, 2017 07:41 |
| Sharing links for two phase solver packages developed by openfoam community | swap_9068 | OpenFOAM Programming & Development | 1 | April 2, 2017 06:43 |
| Wave Action Equation Solver for OpenFOAM | chyczewski | OpenFOAM Programming & Development | 7 | September 4, 2013 12:06 |