 |
|
|
[Sponsors] | |||||
Derivation of Displacement Equation for Solid Stress |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Hello everybody,
I have again some problems with the derivation of the displacement equation for solid stress calculation. I might just have some problems with the Lagrange and Eulerian formulation but however, for me it is not clear. In literature I found the conservation equation for the displacement vector  as: as: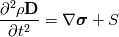 where 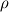 is the density, is the density,  the Cauchy stress tensor and the Cauchy stress tensor and 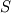 other body forces. This equation can be found in Implementation of solid body stress analysis in OpenFOAM from Tian TANG. The similar equation can be found in the paper of Jasak and Weller named Application of the Finite Volume Method and Unstructured Meshes to linear elasticity. other body forces. This equation can be found in Implementation of solid body stress analysis in OpenFOAM from Tian TANG. The similar equation can be found in the paper of Jasak and Weller named Application of the Finite Volume Method and Unstructured Meshes to linear elasticity.My problem is the time derivative that I don't get. If we start from the momentum equation to derive the displacement equation, I get to the Lagrange formulation and therefore to the Total Derivative of the displacement vector. To demonstrate it, here we go: 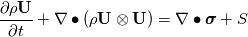 Neglecting the source 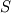 and splitting the time derivative + convective term: and splitting the time derivative + convective term: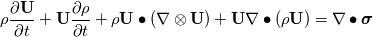 ![\rho\underbrace{\left[\frac{\partial \textbf{U}}{\partial t} + \textbf{U} \bullet (\nabla \otimes \textbf{U}) \right]}_{\text{Total Derivative}} + \textbf{U} \underbrace{\left[ \frac{\partial \rho}{\partial t} +
+ \nabla \bullet (\rho \textbf{U}) \right]}_{\text{continuity = } 0}= \nabla \bullet \boldsymbol \sigma \rho\underbrace{\left[\frac{\partial \textbf{U}}{\partial t} + \textbf{U} \bullet (\nabla \otimes \textbf{U}) \right]}_{\text{Total Derivative}} + \textbf{U} \underbrace{\left[ \frac{\partial \rho}{\partial t} +
+ \nabla \bullet (\rho \textbf{U}) \right]}_{\text{continuity = } 0}= \nabla \bullet \boldsymbol \sigma](/Forums/vbLatex/img/862abce56f3600f69d7009507c8dd8c6-1.gif) 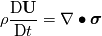 Now introducing the displacement vector (maybe I miss here something): 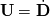 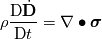 About that step I am not 100% sure 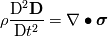 I will check the book Moukalled et al. tomorrow but I am not sure if they talk about stress calculation. It would be nice if someone could highlight my mistakes because if my derivation would be correct, I should change the total derivative into the Eulerian form in order to implement it to FOAM, right? Thanks in advance
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#2 |
|
Member
Brian Willis
Join Date: Mar 2011
Location: Cape Town, South Africa
Posts: 58
Rep Power: 15  |
Hi Tobi
Do we not assume that there is no convective transport term because it is a solid? Regards, Brian |
|
|
|

|
|
|
|
|
#3 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Hi Brian,
I was thinking about that too but if we do so, we get the following:  Therefore the continuity reduces to:  which induces constant density. If that will hold, everything is fine because we get: 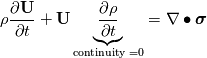 Using the following relation, 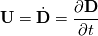 , we get what we get and can see in different literatures: , we get what we get and can see in different literatures: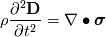 But then we have a constant density. The only thing which will make it density depended is that the continuity is equal to a source term: 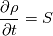 However, then we have to keep the not-vanishing term. But I am not sure if that is correct and how to treat S.
__________________
Keep foaming, Tobias Holzmann Last edited by Tobi; March 14, 2017 at 06:31. |
|
|
|

|
|
|
|
|
#4 |
|
Member
Brian Willis
Join Date: Mar 2011
Location: Cape Town, South Africa
Posts: 58
Rep Power: 15  |
Hi Tobi
Have a look at the derivation in 5.2 of the following notes. Working from Newtons second law of motion applied to the deformation of solids. http://www.brown.edu/Departments/Eng...ation_Laws.htm As to the inclusion of the density term within the time derivative, I cannot say why just yet, unless it is assumed to be constant for the finite volume... Without deriving the NS equation from scratch now, I am guessing some of our assumptions used to find the NS equations may not apply in the derivation for the deformation of solids, hence why you can't find a resolution when starting off with the NS equations and applying to solid deformation. Let me know what you think. Regards, Brian |
|
|
|

|
|
|
|
|
#5 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Hi Brian,
well I think I am doing something wrong, or as you said, some assumptions are not correct. Yesterday I already saw the Brown website but to be honest, I do not like the integral forms too much. However, if we would use the first equation: 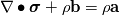 And start from this equation it is obvious (of course). Neglecting body forces and replace the acceleration with 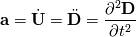 , we will get the equation we can find in literature but it should be a Lagrange formulation, right? , we will get the equation we can find in literature but it should be a Lagrange formulation, right? I also checked out Philip Cardiffs PhD thesis and he is always talking about the Lagrange approach. I feel that I don't know anything :P
__________________
Keep foaming, Tobias Holzmann Last edited by Tobi; March 14, 2017 at 09:38. |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Join Date: Mar 2014
Location: Czech Republic
Posts: 29
Rep Power: 14  |
Hi,
given any field 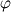 , we write , we write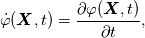 holding 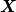 fixed, for its material time-derivative (derivative following the motion) and fixed, for its material time-derivative (derivative following the motion) and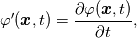 holding 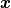 fixed, for its spatial time-derivative. fixed, for its spatial time-derivative.The material time-derivative in spatial (Eulerian) description 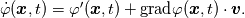 Also, there are conservative and non-conservative forms of balance laws. Conservative form 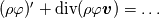 and non-conservative form (assuming the balance of mass holds) 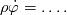 The non-conservative form is especially useful for solids, because we can show that balance of mass is automatically satisfied. The conservative form is severally used in finite volume method (from the nature of the method, ie, fluxes). |
|
|
|

|
|
|
|
|
#7 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Dear Elones,
thanks for your reply. Due to the fact we use FOAM and FVM, and I expect that we have to write the equations in conservative form, I don´t get the point why we directly can write the non-conservative form. If your equations will highlight and solve my issue, I don´t get the point because I still have the problem shown above.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#8 |
|
New Member
Join Date: Mar 2014
Location: Czech Republic
Posts: 29
Rep Power: 14  |
To Dipsomaniac: We do not assume that there is no convective transport term because it is a solid. It comes from mathematical description, in Lagrange (Referential, or Material) formulation there is not convection term, material time-derivative in this formulation is time partial derivative.
To Tobi: 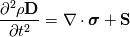 is simply wrong. This is actually little bit complicated and I don't know where to begin. I will try to put this as simple as possible. It "should be" 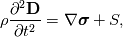 but the trajectory ("displacement") is function of referential coordinates 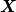 and time and time 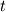 , so on the RHS we have , so on the RHS we have 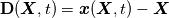 and on the LHS we have Cauchy Stress, which is by the definition, the stress present in the deformed body, ie, and on the LHS we have Cauchy Stress, which is by the definition, the stress present in the deformed body, ie, 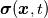 . This equation is only approximation for small deformations, where we can say that Cauchy stress can be though as the stress in the undeformed body. . This equation is only approximation for small deformations, where we can say that Cauchy stress can be though as the stress in the undeformed body.The balance equations in spatial (Eulerian) description (eg fluid mechanics) are the balance of mass conservative 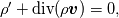 or non-conservative 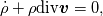 the balance of linear momentum conservative 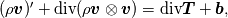 or non-conservative 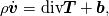 angular moment balance 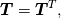 and energy balance non-conservative 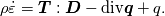 Here, v is the velocity field, rho is the density, T is the Cauchy stress, b is the conventional body force, varepsilon is the specific internal energy, bold q is the heat flux, q is the heat supply and D is the symm grad v and div( . ) = \partial . / \partial x. The correct balance equations in referential (Lagrangian) description are the balance of mass 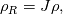 where rho_R is density in referential configuration (say undeformed body) and J is the Jacobian of the deformation; the balance of linear momentum 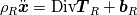 the balance of energy 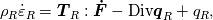 where 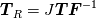 is the Piola stress and F the deformation gradient 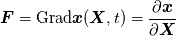 and Div( . ) = \partial . / \partial X. The heat referential flux bold q_R is 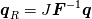 and b_R = J b, q_R = J q. And for small deformation 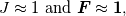 so that 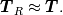
|
|
|
|

|
|
 |
| Tags |
| displacement vector, stress calculation, stress equation |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Stress Equation and Implicit part | Tobi | OpenFOAM | 1 | July 13, 2016 07:25 |
| Simple piston movement in cylinder- fluid models | arun1994 | CFX | 4 | July 8, 2016 03:54 |
| [snappyHexMesh] determining displacement for added points | CFDnewbie147 | OpenFOAM Meshing & Mesh Conversion | 1 | October 22, 2013 10:53 |
| Reynolds Stress equation ??? | Abhijit Tilak | Main CFD Forum | 4 | November 15, 2000 07:01 |
| Derivation of reynolds equation | Mark Harten | Main CFD Forum | 2 | September 9, 1999 12:23 |