 |
|
|
[Sponsors] | |||||
Factors for the cubic inerpolation scheme in OpenFOAM |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: Mar 2017
Posts: 1
Rep Power: 0  |
Dear all,
I have a question regarding the used factors for the cubic interpolation scheme in OpenFOAM. Below you can see a part of the code for the cubic interpolation scheme: Code:
virtual bool corrected() const { return true; } //- Return the explicit correction to the face-interpolate virtual tmp<GeometricField<Type, fvsPatchField, surfaceMesh>> correction ( const GeometricField<Type, fvPatchField, volMesh>& vf ) const { const fvMesh& mesh = this->mesh(); // calculate the appropriate interpolation factors const surfaceScalarField& lambda = mesh.weights(); const surfaceScalarField kSc ( lambda*(scalar(1) - lambda*(scalar(3) - scalar(2)*lambda)) ); const surfaceScalarField kVecP(sqr(scalar(1) - lambda)*lambda); const surfaceScalarField kVecN(sqr(lambda)*(lambda - scalar(1))); tmp<GeometricField<Type, fvsPatchField, surfaceMesh>> tsfCorr ( new GeometricField<Type, fvsPatchField, surfaceMesh> ( IOobject ( "cubic::correction(" + vf.name() +')', mesh.time().timeName(), mesh, IOobject::NO_READ, IOobject::NO_WRITE, false ), surfaceInterpolationScheme<Type>::interpolate(vf, kSc, -kSc) ) ); GeometricField<Type, fvsPatchField, surfaceMesh>& sfCorr = tsfCorr.ref(); for (direction cmpt=0; cmpt<pTraits<Type>::nComponents;cmpt++) { sfCorr.replace ( cmpt, sfCorr.component(cmpt) + ( surfaceInterpolationScheme < typename outerProduct < vector, typename pTraits<Type>::cmptType >::type >::interpolate ( fv::gaussGrad <typename pTraits<Type>::cmptType>(mesh) .grad(vf.component(cmpt)), kVecP, kVecN ) & mesh.Sf() )/mesh.magSf()/mesh.surfaceInterpolation::deltaCoeffs() ); } phi_E=lambda*phi_P+(1-lambda)*phi_N+kSc*phi_P-kSc*phi_N+kVecP*gradPhi_P+kVecN*gradphi_N Here phi_P and phi_N are the values at the owner and neighbor point and gradphi_P and gradphi_N the gradients at the mentioned points.But by the use of a normal cubic polynomial function (f(x)=ax³+bx²+cx+d) for the interpolation of the surface value with given values and gradients for the owner and neighbor points as conditions I get another correlation with the defined factors in the above code: phi_E=lambda*phi_P+(1-lambda)*phi_N-kSc*phi_P+kSc*phi_N-kVecN*gradPhi_P-kVecP*gradphi_N
The differences are the opposite signs and the exchange of the factors. I have tried lot of other numerical interpolation ways to come on the same correlation as used in OpenFOAM but i wasnt sucessful till yet. Does anyone knows how one gets the correlation which is used in OpenFOAM respectively which interpolation technique gives this correlation with the given values and gradients at the owner and neighbor point? Thanks in advance for answers and hopefully someone can give me an advise regarding this problem. |
|
|
|

|
|
|
|
|
#2 |
|
Member
Alexander
Join Date: Mar 2009
Posts: 49
Rep Power: 17  |
I have no deep look into the problem but I am also interesting in that. When lambda is equal to 0.5 both formulas give the same result. Could you post your derivation of the formula please? Of course if it does not cause you any inconvenience

|
|
|
|

|
|
|
|
|
#3 |
|
New Member
Yu Cheng
Join Date: Aug 2014
Posts: 15
Rep Power: 12  |
Hey, guys. I have found the same problem as Hoshang met. I post my derivation of cubic interpolation here, if someone can find any errors, plz feel free to point out.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Given the value of the variable and its gradient at point P and N, assume a cubic polynomial variation in the section PN, derive the variable value at the face f.  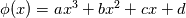 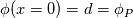 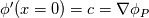 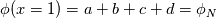 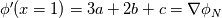 thus a,b,c,d can be solved, 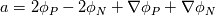 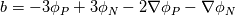 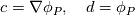 then the variation of 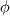 in PN can be expressed as in PN can be expressed as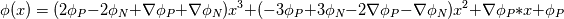 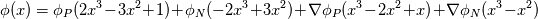 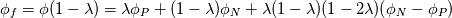 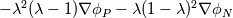 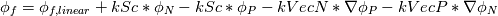 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% The last equation is what exactly Hoshang gave, which is not the same implemented in OpenFOAM. Best wishes Yu Cheng Last edited by chengyu; August 2, 2017 at 22:00. Reason: correct misprint term pointed out by Alexander |
|
|
|

|
|
|
|
|
#4 |
|
Member
Alexander
Join Date: Mar 2009
Posts: 49
Rep Power: 17  |
Hello, Yu Cheng!
I have checked your derivation and found it to be correct, except one misprint in the formula for 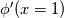 : it should be equal to : it should be equal to 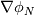 . .I think one should report the bug (https://bugs.openfoam.org/bug_report_page.php). |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Yu Cheng
Join Date: Aug 2014
Posts: 15
Rep Power: 12  |
Yes, you are right, I have changed the original formula, and I think I should better report this to the OpenFOAM official. Thank you.
Best wishes. Yu Cheng |
|
|
|

|
|
|
|
|
#6 |
|
Member
Alexander
Join Date: Mar 2009
Posts: 49
Rep Power: 17  |
Bug report: https://bugs.openfoam.org/view.php?id=2650
|
|
|
|

|
|
|
|
|
#7 |
|
New Member
Yu Cheng
Join Date: Aug 2014
Posts: 15
Rep Power: 12  |
Hi Alexander,
Thank you for the report. Best wishes, Yu Cheng |
|
|
|

|
|
|
|
|
#8 |
|
New Member
Join Date: Apr 2016
Posts: 12
Rep Power: 10  |
Hello everyone!
This is my first post in this awsome forum. I hope this question would not be considered as off-topic, as it is related to the cubic scheme. I started to use openFoam recently, and I'm sure, it is possible to find the answer from the code, but I can't. Therefore I'd gratefull, if anyone could tell me how the gradients are calculated for the cubic scheme. I mean, are the schemes used from fvSchemes, or are they 'hard wired' in the code for this interpolation scheme. Thanks in advance. |
|
|
|

|
|
|
|
|
#9 | |
|
Member
Alexander
Join Date: Mar 2009
Posts: 49
Rep Power: 17  |
Quote:
The scheme for gradient evaluation is hard-coded for cubic interpolation and it is Gauss. |
||
|
|

|
||
|
|
|
#10 | |
|
New Member
Join Date: Apr 2016
Posts: 12
Rep Power: 10  |
Quote:
What do you think, is it possible to change it to fourth for instance? Is it enough to modify the lines: #include "gaussGrad.H" to #include "fourthGrad.H" and >::interpolate ( fv::gaussGrad to >::interpolate ( fv::fourthGrad ? Or use some limiting somehow? |
||
|
|

|
||
|
|
|
#11 | |
|
Member
Alexander
Join Date: Mar 2009
Posts: 49
Rep Power: 17  |
Quote:
|
||
|
|

|
||
|
|
|
#12 |
|
New Member
Join Date: Apr 2016
Posts: 12
Rep Power: 10  |
||
|
|

|
|
|
|
|
#13 |
|
Member
Alexander
Join Date: Mar 2009
Posts: 49
Rep Power: 17  |
I don't look it in deep but I think that you may create your own scheme cubicGrad with runtime-selectable scheme for gradient as it is done for linearUpwind scheme.
|
|
|
|

|
|
|
|
|
#14 |
|
New Member
Join Date: Apr 2016
Posts: 12
Rep Power: 10  |
||
|
|

|
|
|
|
|
#15 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Bad Wörishofen
Posts: 2,711
Blog Entries: 6
Rep Power: 52    |
Hi Sahas,
I read your bug report and the comments. Interesting fact. Right now I could imagine that if you have shock-wave propagation, the results might be different based on the gradients of neighbor/owner which are way much more pronounced in such cases than normal ones. Which cases did you check out for your report?
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#16 | |
|
New Member
Join Date: Apr 2016
Posts: 12
Rep Power: 10  |
Quote:
I have also seen that report. However, I'm not completely sure about my derivation, but if you change how λ is defined above, from f(x=1-λ) to f(x=λ), the same coefficients as implemented in openFoam currently can be derived. |
||
|
|

|
||
|
|
|
#17 | |
|
Member
Alexander
Join Date: Mar 2009
Posts: 49
Rep Power: 17  |
Quote:
I have tried a simple unsteady case of 1D flow with sinusoidal varying velocity at inlet, using uniform and non-uniform grids. The difference between realizations of the cubic scheme is observed only on non-uniform grid and it is quite small (switching to linear or linearUpwind scheme has greater effect). As for shock-wave case, due to the fact that cubic scheme is central scheme it would be hard to get non-oscillating solution for this case. And again, differences in realizations can be only seen on non-uniform grids, where other numerical errors begin to play the role. To summarize, the current implementation gives small errors in a final solution. Perhaps, the effect is strong in the some cases of DNS of turbulence. But DNS is not very suitable to be a simple test case 
|
||
|
|

|
||
|
|
|
#18 | |
|
Member
bany
Join Date: Nov 2019
Posts: 50
Rep Power: 8  |
Quote:
Hi, HoShang. I have a question how "the linear interpolated term plus a correction term" defined in code? I did not find the corresponding code. Thus, I can only turn the code in cubic.H to the following form: phi_E=kSc*phi_P-kSc*phi_N+kVecP*gradPhi_P+kVecN*gradphi_N Any advices are appreciated. |
||
|
|

|
||
|
|
|
#19 |
|
New Member
Lavinia Cummerata
Join Date: Feb 2024
Posts: 4
Rep Power: 2  |
I haven't delved deeply into https://greenleafguru.com the problem, but I'm also interested in it. When lambda equals 0.5, both formulas yield the same result. Could you please share https://herbalhighsociety.com your derivation of the formula? Of course, only if it's not inconvenient for you.
Last edited by Kaley2; May 21, 2024 at 02:53. |
|
|
|

|
|
 |
| Tags |
| cubic, factors, interpolation, scheme, weights |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Getting Started with OpenFOAM | wyldckat | OpenFOAM | 26 | June 21, 2024 07:54 |
| Map of the OpenFOAM Forum - Understanding where to post your questions! | wyldckat | OpenFOAM | 10 | September 2, 2021 06:29 |
| Radiation With View Factors in OPENFOAM | MadiS | OpenFOAM | 1 | August 23, 2012 12:21 |
| Second order upwinding scheme in OpenFoam | subash | OpenFOAM Running, Solving & CFD | 4 | June 20, 2012 19:28 |
| Surface interpolation scheme with tensors as weighting factors | jutta | OpenFOAM Running, Solving & CFD | 1 | August 27, 2007 12:00 |