 |
|
|
[Sponsors] | |||||
A few questions about LES filtering in OpenFOAM |
 12Likes
12Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Yan Zhang
Join Date: May 2014
Posts: 120
Rep Power: 12  |
Hello,
In the OpenFOAM source codes,I found "laplace Filter" in the source codes, so I guessed the dynLagrangian must be used accompany with "laplace Filter". Actually, I am going to implement the dynamic K-E or dynLagrangian SGS model to another software. But I don't know how to implement the "simple Filter". It seems that implementing laplace Filter is more easier. Could you tell me does the SGS models must be used accompany with particular Filters? For example, dynamicKEqn + simple filter; dynamicLagrangian + laplace Filter. Another question: If you understand the meaning of "simple Filter", Could you tell me the physical meaning of it? Please forgive my poor English. simple Filter: tmp<volScalarField> filteredField = fvc::surfaceSum ( mesh().magSf()*fvc::interpolate(unFilteredField) )/fvc::surfaceSum(mesh().magSf()) laplace Filter: tmp<volTensorField> filteredField = unFilteredField() + fvc::laplacian(coeff_, unFilteredField()) Thanks, Zhang Yan [ Moderator note - Moved from here: http://www.cfd-online.com/Forums/mai...-do-you-3.html ] Last edited by wyldckat; May 1, 2016 at 16:01. Reason: see "Moderator note" |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Sep 2015
Location: Singapore
Posts: 102
Rep Power: 11  |
Hi Zhang Yan,
I am trying to figure out LES implementation in OpenFOAM myself but I'll still try to give an answer. Please correct me if I am wrong. simpleFilter If you look at the code, you will see that the unFilteredField is first interpolated from the cell centers to the cell faces using 'fvc::interpolate'. Then, the filteredField is simply the area-weighted average of the interpolated values using 'fvc::surfaceSum'. laplaceFilter I am not so sure about this but I'll try. I'm borrowing some ideas from image processing since that's all the relevant information that I could find on Laplace filters. Let's say you have a random signal,  which has high frequency noise that you wish to filter/smooth. We can derive the finite difference Laplace operator for the signal as: which has high frequency noise that you wish to filter/smooth. We can derive the finite difference Laplace operator for the signal as:  According to the code, the Laplacian is first multiplied by 'coeff_' which is proportional to  and, hence, has the dimensions of and, hence, has the dimensions of  . This result is then added to the unFilteredField. Let's try to do that by letting the proportionality parameter 'widthCoeff_' as 4: . This result is then added to the unFilteredField. Let's try to do that by letting the proportionality parameter 'widthCoeff_' as 4: As it can be seen, the result is an average over the adjacent cells. Conclusion I think filtering operation can be viewed as smoothing or averaging operation. I would love to know if I am getting any of this wrong. Also, I am not too sure as to the role of 'widthCoeff_' and would like to know more as well. As to which filter to use with which dynamic SGS model, I think it does not really matter. Any filter should be fine as long as you define the relevant '<LESFilter>Coeffs'. However, according to this, the laplace filter is not generally used. Not too sure why. Anyway, hope this helps you. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Yan Zhang
Join Date: May 2014
Posts: 120
Rep Power: 12  |
Thank you very much!
Since it's too late today (in my country), I will study your admirable answer carefully tomorrow.
__________________
https://openfoam.top |
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
Yan Zhang
Join Date: May 2014
Posts: 120
Rep Power: 12  |
Quote:
Hi, According to your reply, I got my answer about simple filter: filteredField = sum(A_i * S_i) / sum(S_i) A_i is face value after interpolate, S_i is face area. Is it right? Besides, I have another question: If I use simple filter as the test filter for a dynamic SGS model, as a test filter, how does simple filter show the double width compared to the first filter? Last edited by zhangyan; May 7, 2016 at 07:51. |
||
|
|

|
||
|
|
|
#5 |
|
Senior Member
Join Date: Sep 2015
Location: Singapore
Posts: 102
Rep Power: 11  |
Hi there,
Yup, I have the same idea of the simple filter. I am reading up on filtering myself (I am new to LES/OpenFOAM as well) but here is what I think is happening: The filtering of the original LES equations is implicit in OpenFOAM, i.e. the finite volume method (grid+discretization) itself acts as a filter! This is known as implicit LES. So, when you apply any dynamic model, it performs a further filtering process, the test filter. The factor of two does appear in the code. For example, for the 'homogeneousDynSmagorinsky' model: Code:
const volSymmTensorField MM
(
sqr(delta())*(filter_(mag(D)*(D)) - 4*mag(filter_(D))*filter_(D))
);
![MM_{ij} = \Delta^2 \left[ \widetilde{D_{ij}\sqrt{D_{ij} D_{ij}}} - \frac{\Delta_t^2}{\Delta^2} \widetilde{D_{ij}}{\sqrt{\widetilde{D_{ij}} \widetilde{D_{ij}}}} \right] MM_{ij} = \Delta^2 \left[ \widetilde{D_{ij}\sqrt{D_{ij} D_{ij}}} - \frac{\Delta_t^2}{\Delta^2} \widetilde{D_{ij}}{\sqrt{\widetilde{D_{ij}} \widetilde{D_{ij}}}} \right]](/Forums/vbLatex/img/4a4b4a1d556bf23b2bb0fb5d6e833639-1.gif) where where  . .Hope this helps. Last edited by usv001; May 8, 2016 at 10:37. Reason: Error in formula |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Yan Zhang
Join Date: May 2014
Posts: 120
Rep Power: 12  |
Thanks for your explanation!
Now I am implementing dynamic procedure to KIVA (the software I'm using). In KIVA, velocity is stored on the vertices. So one of the face(bottom) value is : 0.25(u1+u2+u3+u4). Code:
7/--------/|6
/ / |
/ | / |
/ / |
8/--------/5 |
| | | |
| | |
| 3|- -| - |2
| / | /
| | /
| / | /
| |/
4----------1
You know, I must interpolate Sij to the cell faces. For example, S11=dudx, in KIVA, dudx=0.25*(u3+u4+u7+u8-u1-u2-u5-u6)/delta_X I know velocity is stored on the vertice, but I don't know where Sij is stored. So I don't know how to interpolate Sij to the cell faces. Do you have any idea? |
|
|
|

|
|
|
|
|
#7 |
|
Member
Mahdi
Join Date: Jul 2012
Posts: 53
Rep Power: 14  |
Quote:
I agree with this statement that normal LES models use implicit filtering in OpenFOAM. Also dynamic models use explicit filter (with different choices for shape and size) as the test filter. But if you check the code for one of the dynamic models like "Dynamic Smagorinsky" they use the same delta that is used in normal "Smagorinsky" which is implicit. Isn't it contradictory? Because as you showed in the equation above, the factor 4 appears because the test filter width (explicit) is twice the grid filter (implicit), but what we see as the delta in both models is grid size (i.e. cuberoot ---> deltaCoeff_*pow(mesh().V(), 1.0/3.0) ) and this delta coefficient is always 1 in every "LESProperties". Do you have any comment on that? |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Join Date: Sep 2015
Location: Singapore
Posts: 102
Rep Power: 11  |
Hello Mahdi,
My understanding is that if you don't use any SGS model, then you are letting the inherent numerical dissipation to play its place. So, under this definition the Smagorinsky model is not an implicit LES but an explicit one - you specify an SGS model. So, I see no issues in the SGS models (Smagorinsky and its dynamic counterpart) using the same delta. The only thing that matters is that the test filter width  must be larger than the normal filter width must be larger than the normal filter width 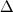 . However, I am no expert in this area. So, correct me if I wrong about any of this. . However, I am no expert in this area. So, correct me if I wrong about any of this.Cheers, USV |
|
|
|

|
|
|
|
|
#9 |
|
Member
Mahdi
Join Date: Jul 2012
Posts: 53
Rep Power: 14  |
Quote:
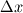 for as the filter width, or not? for as the filter width, or not?That's why we do not see any "filter" in the formulation of, for instance, Smagorinsky. But when you check the code of "dynSmagorinsky" or "dynOneEddy", the term "filter" is clearly seen in the code. This is of course the "test" filter, and its type is usually chosen "simple". But it uses the same width. So, the crucial condition of "  " doesn't get satisfied. Isn't it a problem? " doesn't get satisfied. Isn't it a problem?Or you mean the 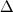 in the turbulence model and filter width are two different entities? in the turbulence model and filter width are two different entities?
|
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Fumiya Nozaki
Join Date: Jun 2010
Location: Yokohama, Japan
Posts: 266
Blog Entries: 1
Rep Power: 19  |
Hi Mahdi,
I have the same question and am thinking in the following manner. In the simple filter, the fvc::interpolate function is used to calculate the filtered field, so the neighbour cells' values are considered in the test filtering operation and  is satisfied. is satisfied.Best regards, Fumiya
__________________
[Personal]
|
|
|
|

|
|
|
|
|
#11 | |
|
Member
Mahdi
Join Date: Jul 2012
Posts: 53
Rep Power: 14  |
Quote:
it is still unclear to me how to determine the width of filter/stencil. In other words, is the width now twice the grid size? Because by interpolation I still see the delta_t = grid size. Or I am mistaken? |
||
|
|

|
||
|
|
|
#12 |
|
Senior Member
Agustín Villa
Join Date: Apr 2013
Location: Alcorcón
Posts: 314
Rep Power: 15  |
Hello to everybody, I will float again this thread, since now I have some doubts. I will set my points:
Agustin |
|
|
|

|
|
|
|
|
#13 | |
|
Senior Member
Yan Zhang
Join Date: May 2014
Posts: 120
Rep Power: 12  |
Quote:
|
||
|
|

|
||
|
|
|
#14 | |
|
Member
Mahdi
Join Date: Jul 2012
Posts: 53
Rep Power: 14  |
Quote:
Therefore, what you give as a user input parameter in the turbulence dictionary as "delta" is the representative of grid filter size or delta_g But the delta that you use in the dynamic models is the width of "test" filter not grid filter. It is usually considered twice the grid filter i.e. delta_t = 2*delta_g. So, again you would need only delta_g, because you can simply multiply it by factor 2 where you need "test" filter. I mean the factor 2 can be automatically considered in the formulation of dynamic models (For instance, see the factor 4 in the formula of MM in dynamic Smagorinsky ). |
||
|
|

|
||
|
|
|
#15 | ||
|
Senior Member
Agustín Villa
Join Date: Apr 2013
Location: Alcorcón
Posts: 314
Rep Power: 15  |
Quote:
Quote:
 Where  They talk about using a coarser width, but I don see how to follow the analogy with the dynamic Smagorinsky. Cv is constant. If there was a way to specify a width directly to the filter... |
|||
|
|

|
|||
|
|
|
#16 |
|
Senior Member
Agustín Villa
Join Date: Apr 2013
Location: Alcorcón
Posts: 314
Rep Power: 15  |
Another point is: where the delta is used in the code of the filters?
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Frequently Asked Questions about Installing OpenFOAM | wyldckat | OpenFOAM Installation | 3 | November 14, 2023 12:58 |
| LES filter in OpenFOAM | openfoammaofnepo | OpenFOAM Programming & Development | 1 | October 23, 2014 08:27 |
| implicit and explicit filtering in LES | kkpal | OpenFOAM | 0 | February 19, 2014 03:27 |
| Molecular viscosity calculation in LES on OpenFOAM | babakflame | OpenFOAM | 0 | January 26, 2014 05:13 |
| Serious bug in LES interface | fs82 | OpenFOAM Bugs | 21 | November 16, 2009 09:15 |