 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Sep 2014
Posts: 15
Rep Power: 12  |
Hello foamers!
I have two equations (assume p and T are dimensionless volScalarFields) 1)  2)  I already know  and and  , ,  The first equation is easy: Code:
fvScalarMatrix pEqn ( fvm::ddt(p) + p ); pEqn.solve(); 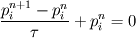 Now I know  for all for all  If I write the second equation using finite differences, I will get  But what is the analogue of this equation in OpenFOAM? If I try to use Code:
fvm::ddt(p,T) + T 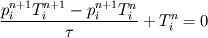 So how to use OpenFOAM correctly here? Please help! |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
|
||
|
|

|
|
|
|
|
#3 |
|
Member
Mattia de\' Michieli Vitturi
Join Date: Mar 2009
Posts: 51
Rep Power: 17  |
Hi,
are you sure that about this? I've always tought that ddt(p,T) discretizes the derivative in time of pT. Otherwise, if it was p times the temporal derivative of T, why not using p*ddt(t)? Also looking at Table 2.2 of the programming guide it seems that ddt(p,T) should be the discretization of the time derivative of (p*T). Can you clarify it? Thank you Mattia |
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
Mohammad Shakil Ahmmed
Join Date: Oct 2012
Location: AUS
Posts: 137
Rep Power: 15  |
Quote:
Cheers shakil |
||
|
|

|
||
|
|
|
#5 |
|
New Member
Join Date: Sep 2014
Posts: 15
Rep Power: 12  |
||
|
|

|
|
|
|
|
#6 |
|
Senior Member
|
Well,
Here fvc::ddt method in EulerDdtScheme: Code:
template<class Type>
tmp<GeometricField<Type, fvPatchField, volMesh> >
EulerDdtScheme<Type>::fvcDdt
(
const dimensionedScalar& rho,
const GeometricField<Type, fvPatchField, volMesh>& vf
)
{
dimensionedScalar rDeltaT = 1.0/mesh().time().deltaT();
IOobject ddtIOobject
(
"ddt("+rho.name()+','+vf.name()+')',
mesh().time().timeName(),
mesh()
);
if (mesh().moving())
{
...
}
else
{
return tmp<GeometricField<Type, fvPatchField, volMesh> >
(
new GeometricField<Type, fvPatchField, volMesh>
(
ddtIOobject,
rDeltaT*rho*(vf - vf.oldTime())
)
);
}
}
Code:
template<class Type>
tmp<fvMatrix<Type> >
EulerDdtScheme<Type>::fvmDdt
(
const volScalarField& rho,
const GeometricField<Type, fvPatchField, volMesh>& vf
)
{
...
scalar rDeltaT = 1.0/mesh().time().deltaTValue();
fvm.diag() = rDeltaT*rho.internalField()*mesh().Vsc();
if (mesh().moving())
{
...
}
else
{
fvm.source() = rDeltaT
*rho.oldTime().internalField()
*vf.oldTime().internalField()*mesh().Vsc();
}
...
}
|
|
|
|

|
|
|
|
|
#7 |
|
Member
Mattia de\' Michieli Vitturi
Join Date: Mar 2009
Posts: 51
Rep Power: 17  |
The correct formula is the first one. Take a look at the programmers guide (page 37 for version 2.3.1) and you will find everything. Eq. 2.21 is exactly what you are looking for.
Mattia |
|
|
|

|
|
|
|
|
#8 |
|
New Member
Join Date: Sep 2014
Posts: 15
Rep Power: 12  |
I am not sure that I understand
 correctly... correctly...I think that in the beginning of the time loop (p and T are dimensionless volScalarFields) we have formula below:  But after solving this equation: Code:
fvScalarMatrix pEqn ( fvm::ddt(p) + p ); pEqn.solve();  So  ? ?I mean when we use  , rho always behaves like a scalar, right? , rho always behaves like a scalar, right?Please correct me, if I am wrong. |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
|
It behaves like scalar field i.e. it can vary in space.
|
|
|
|

|
|
|
|
|
#10 |
|
New Member
Join Date: Sep 2014
Posts: 15
Rep Power: 12  |
||
|
|

|
|
|
|
|
#11 |
|
New Member
Join Date: Sep 2014
Posts: 15
Rep Power: 12  |
Hi, I have a new big problem with temporal derivative!
Again, A and B are dimensionless volScalarFields I also have Code:
dimensionedScalar c ("c", dimensionSet(0, 0, 1, 0, 0, 0 ,0), 1.0);
 and and  , ,  I solved the first equation: Code:
fvScalarMatrix AEqn
(
c*fvm::ddt(A) + A
);
AEqn.solve();
 Now I know  and and  , ,  After that I tried to solve the second equation: Code:
fvScalarMatrix BEqn
(
c*fvm::ddt(A) +c*fvm::ddt(B) + B
);
BEqn.solve();
Code:
--> FOAM FATAL ERROR : incompatible fields for operation [A] + [B]  in the first equation! in the first equation! How can I tell him that? Thank you very much for any hint ... |
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
|
Hi,
fvm:: methods usually operate on the same field, so OpenFOAM is not quite happy about your fvm::ddt(A) + fvm::ddt(B). If you need time derivative of A in equation for B, you can use it as a source term with fvc::ddt(A). So your code should be: Code:
fvm::ddt(B) + B/c + fvc::ddt(A) |
|
|
|

|
|
|
|
|
#13 |
|
New Member
Join Date: Sep 2014
Posts: 15
Rep Power: 12  |
alexeym, exactly, I need to use fvc::ddt(A) in my equation...
Thanks a lot! |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Elastic or Plastic Deformations in OpenFOAM | NickolasPl | OpenFOAM Pre-Processing | 36 | September 23, 2023 09:22 |
| AMI speed performance | danny123 | OpenFOAM | 21 | October 24, 2020 05:13 |
| simpleFoam error - "Floating point exception" | mbcx4jc2 | OpenFOAM Running, Solving & CFD | 12 | August 4, 2015 03:20 |
| Moving mesh | Niklas Wikstrom (Wikstrom) | OpenFOAM Running, Solving & CFD | 122 | June 15, 2014 07:20 |
| Micro Scale Pore, icoFoam | gooya_kabir | OpenFOAM Running, Solving & CFD | 2 | November 2, 2013 14:58 |