 |
|
|
[Sponsors] | |||||
Setting boundary conditions to faces, really simple question |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
lazio
Join Date: Apr 2010
Posts: 22
Rep Power: 16  |
Hi,
I am just wondering a very basic principle. If the linear system of equations is set up for each cell in the domain from the well known equation (where p is the cell center and n the neighbouring cell centres):  Where are the boundary condition imposed, considering BC's are to be set at the appropriate faces and the values for 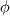 are at the cell centers? are at the cell centers?
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
duri
Join Date: May 2010
Posts: 245
Rep Power: 17  |
You can set up boundary conditions by two ways. In Ghost cell approach boundary values are stored in the ghost cells which is adjacent to boundary. Boundary fluxes are calculated from interior and ghost cell. Other way is to apply characteristics boundary condition where you can do it directly on face and estimate flux without additional cells.
|
|
|
|

|
|
|
|
|
#3 | |
|
New Member
lazio
Join Date: Apr 2010
Posts: 22
Rep Power: 16  |
Quote:
I take then that the setting of a fixed value boundary ( e.g.,  ) is done implicitly through either of the methods you mentioned above and there is no explicit imposing of ) is done implicitly through either of the methods you mentioned above and there is no explicit imposing of  within the algebraic system of equations? within the algebraic system of equations?
|
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
|
Besides the specific approach in use, in cell centered FV method you have variables stored in cell centers but you need their integrals on volume faces. When they are available they are used directly (velocity and/or mass flow inlets; wall normal derivative of the wall normal velocity component for incompressible flows; symmetry boundaries; outflows etc). In all the other cases, both on boundary and interior cells, some reconstruction/approximation is adopted by using known face or neighbor cell values.
|
|
|
|

|
|
|
|
|
#5 | |
|
New Member
lazio
Join Date: Apr 2010
Posts: 22
Rep Power: 16  |
Quote:
Thank you for your explanation Paolo, if you don't mind I want to write in my understanding and if you or anyone could please comment/correct? In the cell centered FV method the variables are stored at the cell centers but the face values are required for the discretized forms of the convection and diffusion terms. Generally this is obtained by interpolation such as the popular upwind differencing. At a fixed value (Dirichlet) boundary this is set directly to the specified value (no interpolation is used). This results in the correct value being obtained for the boundary without direct modification of the algebraic system of equations. Subsequently, the setting of a fixed value boundary condition is more complex than directly imposing  in in ![[A] [\phi] = [Q] [A] [\phi] = [Q]](/Forums/vbLatex/img/99072bb556e955330e49714df4d2e3f5-1.gif) , but is achieved through setting values at the faces where they are used in the discretized form of the equations which results in a modification of the coefficient matrix ( , but is achieved through setting values at the faces where they are used in the discretized form of the equations which results in a modification of the coefficient matrix (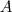 ) and source vector ( ) and source vector ( ). ).
|
||
|
|

|
||
|
|
|
#6 |
|
Senior Member
|
Dear lrunber,
you are essentially correct, however i'd like to stress some aspects. 1) When you put your equations under the matrix form, you have to remember that this implies that your variables are the cell centerd ones (in cell centered FV). As a consequence, using a face variable directly (a la Dirichlet) actually implies a modification in the corresponding cell equation (i assume there is only one neighbor cell as it is a boundary condition) with respect to other interior cell equations. That is, the corresponding neighbor cell coefficient is missing from the relative equation in the system. 2) In a general transport equation, face values are required for the variables and their face normal gradient. As you can only have one boundary condition (dirichlet or neumann, respectively), one of the two values required still need an approximation involving other cell values. Say, you have a dirichlet condition: the boundary normal gradient has to be approximated by values inside the domain (one-sided, in contrast to the ghost-cell approach). If you have a neumann condition then the face values will need an approximation involving interior cells (however, face values in finite volumes are only required for the convective term and this case has very few applications, mostly outflows) Hope this helps more |
|
|
|

|
|
|
|
|
#7 | |
|
New Member
lazio
Join Date: Apr 2010
Posts: 22
Rep Power: 16  |
Quote:

|
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Wind turbine simulation | Saturn | CFX | 60 | July 17, 2024 06:45 |
| [snappyHexMesh] SnappyHexMesh for internal Flow | vishwa | OpenFOAM Meshing & Mesh Conversion | 24 | June 27, 2016 09:54 |
| DecomposePar unequal number of shared faces | maka | OpenFOAM Pre-Processing | 6 | August 12, 2010 10:01 |
| Reading field values and setting them as boundary conditions | sega | OpenFOAM Running, Solving & CFD | 1 | July 7, 2009 07:18 |
| help setting up boundary conditions for combustor | Tomas | CFX | 2 | November 3, 2005 04:34 |