 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Dan
Join Date: Oct 2010
Location: UK
Posts: 41
Rep Power: 16  |
||
|
|

|
|
|
|
|
#2 |
|
Member
|
Hi
The first one corresponds to non-dimensonalized equations, and the second one in dimensional form |
|
|
|

|
|
|
|
|
#3 |
|
Member
Dan
Join Date: Oct 2010
Location: UK
Posts: 41
Rep Power: 16  |
I presume then if I am creating a finite volume solver for unsteady flows over complex geometries, I need the dimensional form.
Yet many authours seem to be usind the non-dimentionalized formulation. Come to think of it did strike me as odd when in ("Numerical Simulation in Fluid Dynamics,A practical introduction", Griebel et al; 1998) The authour seemed to be sugesting the use of the first form over complex geometries, where a  for the definition of Re would be hard to define. for the definition of Re would be hard to define.Dan |
|
|
|

|
|
|
|
|
#4 |
|
Member
Dan
Join Date: Oct 2010
Location: UK
Posts: 41
Rep Power: 16  |
I have also come across a third form of the viscous term
 ("Benchmark Computations of Laminar Flow around a Cylindr", Schafer and Turek; 1996, Notes on numerical dluid mechanics; 52, 547-566) ("Incompressibel Fluid Dynamics", Hunt; 1964) this seems to relate directly to the visous fluid stress tensor,  ("Introduction to computational fluid dynamics", Date; 2005) as far as I can tell this adds another three elements to the viscous term, so for a three dimensional flow the term would be,  the connection to the stress tensor seems logical, however I cand seem to find a direct derivation. Inconsistancy between available literature sources seems to be sending me in circles, Can anyone help me figure out which formulation I need? Dan |
|
|
|

|
|
|
|
|
#5 |
|
Administrator
Peter Jones
Join Date: Jan 2009
Posts: 682
Rep Power: 10  |
The same equation can be written in many ways. CFD Wiki provides a more general dimensional form, which is valid for compressible flows (some of your examples assume incompressible flow):
http://www.cfd-online.com/Wiki/Navier-Stokes_equations |
|
|
|

|
|
|
|
|
#6 |
|
Member
Dan
Join Date: Oct 2010
Location: UK
Posts: 41
Rep Power: 16  |
Hi Pete,
I'm still strugelling to see the equivelence the link you posted gave the viscos term for the ith dimension as,  which agrees with the formulation in my last post, yet how can this be equivelent to the formulations in my original post, if the entire rest of the equation of momentum matches up, except for the three added terms, 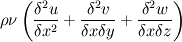 Unless these terms all cancel out to zero..or I'm simpy interpreting the notation incorrectly. |
|
|
|

|
|
|
|
|
#7 |
|
Member
|
Hi
your \tau_{ij} term has a missing term. According to stokes hypothesis for a Newtonian fluid \tau_{ij} = \left( \frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i} - \frac{2}{3}\frac{\partial u_i}{\partial x_j}\delta_{ij} and apply divergence to this quantity |
|
|
|

|
|
|
|
|
#8 |
|
Member
Dan
Join Date: Oct 2010
Location: UK
Posts: 41
Rep Power: 16  |
Tank you Ramesh
 where presumably  is the Kronecker delta, given as, is the Kronecker delta, given as, (Childers; 1981) Making 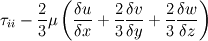 this will add the aditional terms,  Reducing the overall discrepency with the formulations in my original post to, 
Last edited by dandalf; November 18, 2010 at 10:56. Reason: correction |
|
|
|

|
|
|
|
|
#9 |
|
New Member
Francisco Angel
Join Date: Dec 2012
Posts: 26
Rep Power: 14  |
Quote:

|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| 4th order Runge-Kutte & uncoupled method Navier Stokes equations | misabel | Main CFD Forum | 0 | February 10, 2010 07:06 |
| Navier Stokes equations in rotation frame..? | vinayender | Main CFD Forum | 2 | December 1, 2009 01:12 |
| LBM Vs navier stokes equations in turbulent fluid flow modeling. | sharad_shevate | Main CFD Forum | 0 | August 3, 2009 02:25 |
| Incompressible Navier stokes with source term | mayur | FLUENT | 0 | August 6, 2004 07:07 |
| Presure range of the Navier Stokes Equations | Dr. Tsimento | Main CFD Forum | 7 | May 23, 2001 11:12 |