 |
|
|
[Sponsors] | |||||
difference between isotropic and homogeneous in turbulence |
 17Likes
17Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: Feb 2010
Posts: 12
Rep Power: 16  |
Some literature wrote that 'One might argue that no real turbulent flow is isotropic or even homogeneous in the large scales.'
It sounds that homogeneous is stricter than isotropic! SO who can give me any hints about the difference between isotropic and homogeneous? Any comments will be appreciated. |
|
|
|

|
|
|
|
|
#2 |
|
Member
ganesh
Join Date: Mar 2009
Posts: 40
Rep Power: 17  |
Dear Dut_thinker,
Isotropic turbulence demands that there is no mean shear, rotation or buoyancy effects in the flow as this can lead to anisotropy. Homogeneous turbulence is indicative of the fact that there are no mean flow gradients. In a more simpler sense, homogeneity deals with invariance in translation, isotropy deals with invariance in rotation. Take a look at MIT OCW notes on turbulence if you wish for more information. Regards, Ganesh |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Join Date: Apr 2009
Posts: 159
Rep Power: 17  |
||
|
|

|
|
|
|
|
#4 |
|
Senior Member
Join Date: Feb 2010
Posts: 148
Rep Power: 17  |
Thanks f-w! This link is very helpful! I'm typing the information below in case the book disappears.
In homogeneous turbulence, the fluctuating velocity field u(x,t) is statistically homogeneous. It is consistent with this definition for the mean velocity gradients d(Ui)dxj to be non-zero but uniform. A good approximation to homogeneous turbulence can be achieved in wind-tunnel experiments and homogeneous turbulence is the simplest class of flows to study using DNS. A statistically homoegeous field U(x,t) is, by definition, statistically invariant under translations (i.e. shifts in the origin of the coordinate system). If the field is also statistically invariant under rotations and reflections of the coordinate system, then it is (statistically) isotropic. Reference: Turbulent Flows by S. B. Pope |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Join Date: Oct 2010
Posts: 7
Rep Power: 16  |
An isotropic turbulent flow as other members have already replied, is basically a turbulent flow where the time averaged turbulent quantities ( like u r.m.s.) have the same value at each and every location.
A homogeneous flow on the other hand is one where the turbulent quantities at any given location are the same in all the directions. (ex. u r.m.s = v r.m.s.) example a concrete wall may be isotropic if the concentration of steel and cement is the same at all locations in the wall. But it is not homogeneous because at any point, there may be steel in one direction and cement in the other direction. Of course it is actually impossible to get either homogeneous or isotropic turbulence in a wind tunnel. But you can get close to it and ppl want to get close to it cause theoretically a homogeneous isotropic turbulence is very attractive. And ya it is much more impossible to get actual 100% isortopic turbulence cause turbulent flows are by definition dissipative. So the turbulent quantities ( like u r.m.s.) will decay into heat energy with time. Unless you the right amount of energy at the right time it will not be isotropic. |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Join Date: Jan 2013
Posts: 1
Rep Power: 0  |
simulationman, Is definition of homogeneous and isotropic in your answer switched maybe?
|
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
just to make an example, often the turbulence in channel flow is simulated, the test is composed by two parallel plates that are replicated by periodic boundary conditions. The flow is substained by a forcing pressure gradient.
This flow is simultaneously homogeneous along the two directions of periodicity and inhomogeneous in the direction normal to walls |
|
|
|

|
|
|
|
|
#8 |
|
New Member
Nick
Join Date: Oct 2013
Posts: 2
Rep Power: 0  |
Homogeneous turbulence: invariance in translation
Isotropic turbulence: invariance in rotation |
|
|
|

|
|
|
|
|
#9 | ||
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Quote:
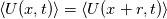 then, the gradient 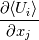 be non-zero?!! I mean it MUST be zero! Quote:
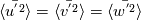 I think this issue has nothing to do with mean shear! Then why mean shear is zero?! |
|||
|
|

|
|||
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
Plane channel flow is an example of flow homogeneous in the streamwise direction while being non-homogeneous in normal direction. It has dU/dy different from zero. |
|
|
|

|
|
|
|
|
#11 | |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Quote:
Plane channel flow is a partially homogeneous flow (in x and z directions). I think the author is talking about a totally homogeneous flow (in every direction). Also, if the flow is homogeneous in one direction, it does not mean that velocity must have a constant gradient in other non-homogeneous directions. |
||
|
|

|
||
|
|
|
#12 |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
I think these statements are the best definitions of isotropic and homogeneous turbulent flow:
A turbulent flow is said to be isotropic if:
A turbulent flow is said to be homogeneous if:
[MIT OCW] |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| axisymmetric homogeneous isotropic turbulence | RAJANI | Main CFD Forum | 1 | April 24, 2006 07:44 |
| the homogeneous isotrotic compressible turbulence. | loong | Main CFD Forum | 0 | March 30, 2006 01:18 |
| Help needed on homogeneous isotropic turbulence an | Guoping Xia | Main CFD Forum | 0 | March 12, 2006 22:54 |
| ISOTROPIC HOMOGENEOUS TURBULENCE | Valdemir | Main CFD Forum | 2 | September 2, 2003 00:04 |
| isotropic homogeneous turbulence | tingguang | Main CFD Forum | 0 | August 1, 2002 18:08 |