 |
|
|
[Sponsors] | |||||
Riemann-Solver/problems + Finite Volume schemes |
 6Likes
6Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: May 2009
Posts: 24
Rep Power: 17  |
Hi,
I have a question concerning approx. Riemann-solvers. As far as I understood from literature, approximate Riemann-solvers (for instance by Roe) solve the Riemann-problem to reconstruct the vector of conservative values which is needed to compute the flux F_i+/- 1/2. What confuses me a little is the point, that the mathematical problem of the Riemann-solver is formulated in the divergence form. I always thought that jump problems can only be captured by the integral form. |
|
|
|

|
|
|
|
|
#2 |
|
Member
Jed Brown
Join Date: Mar 2009
Posts: 56
Rep Power: 19  |
Finite volume methods should never use the differential form, it is just a convenient notation and you should always interpret it as the corresponding weak form. The Roe solver linearizes
 because because 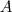 is taken to be constant. The last is natural for finding characteristics, but after finding characteristics, you are still morally working with the weak form of is taken to be constant. The last is natural for finding characteristics, but after finding characteristics, you are still morally working with the weak form of  with discontinuous with discontinuous  . Of course the linearization is precisely the reason that Roe schemes require an entropy fix. . Of course the linearization is precisely the reason that Roe schemes require an entropy fix.
|
|
|
|

|
|
|
|
|
#3 |
|
New Member
Nicholas F Camus
Join Date: Sep 2009
Location: London, England.
Posts: 21
Rep Power: 17  |
Dear PCFD,
The whole point of a Riemann solver as you rightly point out is to determine the intercell numerical fluxes, which can be used in some scheme to update the appropriate cells. The point is that merely using the Jacobian matrix A (a function of non-conservative variables) to determine the fluxes for a conservative scheme can be problematic - this problem is not so relevant for low Mach numbers, but is prevalent at high velocities. In addition the componants of the matrix it self can be complex functions of varibles, and this is where Roe type solvers come in which use the Linearised matrix B, say. This matrix uses the linearised form of the matrix A and it's componants. The use of Riemann solvers these days, are more often than not used in conjuction with a Godunov type scheme. These schemes involve the integral equations of the system of conservation laws under consideration, and the Riemann problem (and solutions to it), which are used to obtain the interface fluxes. There are essentially two ways of finding these so-called intercell numerical or "Godunov" fluxes via a Riemann problem: 1. To find an approximation to the physical state U in each cell and use this to calculate the intercell fluxes F. 2. To find an approximation to F directly without solving Riemann problems. Approximate Riemann solvers like HLL etc. used method 2., whereas Roe-type linearised solvers use 1. The whole point of Riemann solvers is to get approximations (or exact solutions in some cases) to the intercell fluxes. |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Nicholas F Camus
Join Date: Sep 2009
Location: London, England.
Posts: 21
Rep Power: 17  |
One other quick point:
Linearised Solvers like Roe's etc. solve for the right eigenvectors of the Jacobian matrix A. These methods subsequently can resolve the jumps accross each wave of the system underconsideration (hydrodynamic/relativistic hydrodynamic, MHD/relativistic MHD etc.), and there is always one wave associated with each variable of the system. So for hydrodynamics we have three, MHD we have seven. Approximate solvers like HLL do not resolve all the waves of the system, hence jumps in the state vector across them (HLL uses the fastest and slowest wave speeds). This blends the solution at the important point (at the cell interface where you want to know the value of the fluxes) into one - making these scheme very diffusive... The Rieman problem is an initial boundary value problem that starts with the state vector differeing in two cells (the cell interface). The Riemann solver's job is to find at some later time, the difference in the state vector in these two cells. Due to the nature of the problem and hyperbolic system the situation results in the probagation of waves (information), each wave involving a change in the state vector across its surface. We then need to work out what changes have occured to the state vectors at the cell interface due to the wave propagation. Neglecting these wave subsequently reduces the accuracy of you solver. Using the solution, you can then use the numerical method you have adopted to advance the flow/solution in time. Cheers, Killercam E. F. Toro (1999) perhaps is a good bok to used to understand these methods. |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Join Date: Apr 2010
Posts: 20
Rep Power: 16  |
Hi everyone,
I am looking for equations of Riemann solvers on finite volume. My boss tells me that they work only on the normal of the face but I don't trust him. Can someone tell me if I can calculate the Riemann flux without changing my freame of reference to the normal of the face? I want to use Lax Wendroff approach, first to calculate the flux vector and then multiply with the normal of the surface. Thanks, Emre |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Nicholas F Camus
Join Date: Sep 2009
Location: London, England.
Posts: 21
Rep Power: 17  |
Yes. You need the fluxes normal to the cell faces, but this does not require a change of reference frame. if you have an unstructured mesh you can trivially calculate the surface normals hence the direction of the fluxes. So you have the right idea.
Lax-Wen is garbage. Try using the HLL or HLLC solver, the HLL is very simple and should give much better results. Hope this helps. Cam |
|
|
|

|
|
|
|
|
#7 |
|
New Member
Join Date: Apr 2010
Posts: 20
Rep Power: 16  |
So I can calculate flux on N-Dimension and then finally multiply the flux vector with the normal vector?
Do you have any article on 3D Riemann Solvers? The articles I found are all for 1D. Thanks |
|
|
|

|
|
|
|
|
#8 |
|
New Member
Nicholas F Camus
Join Date: Sep 2009
Location: London, England.
Posts: 21
Rep Power: 17  |
There are many. Try Mingnone & Bodo HLL Scheme for gas dynamics - use a shearch engine to find it. Alternatavly use a book by E. F. Toro 1997 Riemann Solvers...?
The Riemann Solver (RS) is inherintly a 1D numerical recipie. It calculates the intercell fluxes for a 1D local interface. Once this is working you just call this routine for each dimension in the respective directions for your scheme. If for e.g. I was on a 2D spherical mesh, I would first do all my theta-integrations, using the RS, then do the radial directions, calling the same riemann solver - the physics is not changing in the respective directions - why should the RS. I hope this helps bud... One you have all the Fluxes in the 2 directions you can then use your Godunov Scheme or what ever your method to update all your cells in the mesh... |
|
|
|

|
|
|
|
|
#9 | |
|
Senior Member
Reviewer #2
Join Date: Jul 2015
Location: Knoxville, TN
Posts: 141
Rep Power: 11  |
Quote:
|
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| finite volume VS finite element | solomon | FLUENT | 4 | April 3, 2015 01:10 |
| [blockMesh] BlockMesh FOAM warning | gaottino | OpenFOAM Meshing & Mesh Conversion | 7 | July 19, 2010 15:11 |
| On the damBreak4phaseFine cases | paean | OpenFOAM Running, Solving & CFD | 0 | November 14, 2008 22:14 |
| fluent add additional zones for the mesh file | SSL | FLUENT | 2 | January 26, 2008 12:55 |
| [blockMesh] Axisymmetrical mesh | Rasmus Gjesing (Gjesing) | OpenFOAM Meshing & Mesh Conversion | 10 | April 2, 2007 15:00 |