 |
|
|
[Sponsors] | |||||
Derivation of Equation in Paper(Kim&Moin 1987, Turbulence) 1 |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
-
Join Date: Oct 2021
Location: -
Posts: 139
Rep Power: 5  |
Hello everyone
I'm reading paper entitled by 'Turbulence statistics in fully developed channel flow at low Reynolds number' by Kim & Moin. (https://www.researchgate.net/publica...eynolds_Number) While reading paper, there were several things that I can't understand from the beginning. So to ask questions about that I've posted thread. Please refer attachment. 1. It is written that both convective terms and mean pressure gradient are included in 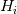 . But I can't understand why mean pressure gradient is include at there. At first, pressure term is already written by . But I can't understand why mean pressure gradient is include at there. At first, pressure term is already written by 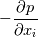 . Secondly, because we're dealing with Navier Stokes eqn rather RANS, what we have to consider is instant pressure, not mean pressure. But why mean pressure gradient is included in . Secondly, because we're dealing with Navier Stokes eqn rather RANS, what we have to consider is instant pressure, not mean pressure. But why mean pressure gradient is included in 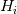 ? ? Why mean pressure is included in Why mean pressure is included in 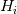 ? ?2. It is written that eqn 3 and 4 are derived from eqn 1(Navier Stokes) and 2(Continuity). But derivation is skipped. It is only written that eqn 3 and 4 are derived by reducing eqn 1 and 2. Where can I find derivation process?  I want to know derivation of eqn 3 and 4 I want to know derivation of eqn 3 and 43. Why eqn 3 and 4 are needed? As far as I know, what we need to solve is just only continuity eqn and Navier Stokes eqn which is governing eqn. But why are we treating irrelavent things such as eqn 3 and 4? Actually I've taken glance at next part slightly and I guessed if eqn 3 and 4 are necessary, then it would be used for numerical calculation. Is it right? If so, I can understand eqn 3 might be needed because it is related to momentum which is quantity of Navier Stokes eqn. But, still, I can't understand why eqn 4 is required. Eqn 4 is related to vorticity which is not a quantity of governing equation. Nonetheless why do we need it?  Reason of introducing eqn 3 and 4 Reason of introducing eqn 3 and 44. Spectral method is written in upcoming paragraph. Is spectral method used for numerical method also? When I learned SIMPLE algorithm briefly, spectral method or kind of Fourier series is not used if I remember correctly. Is spectral method used for CFD calculation also?  Is spectral method used for CFD? Is spectral method used for CFD?Thank you for reading |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,753
Rep Power: 66    |
1. This is a common formulation for streamwise periodic channel flows (i.e. fully developed channel flows). The mean pressure gradient is what drives the flow in such a scenario and hence it can be absorbed into a uniform source. Doing so allows you to apply periodic BC's for the resulting modified pressure, which is what you want to do for a periodic flow. Otherwise, you have to apply an upstream pressure and downstream pressure BC at the inlet and outlet and these have to be spatially and temporally accurate for DNS. You have no clue what the instatantaneous pressure profile over the boundary needs to be at every timestep
2&3. Fully developed flows are a degenerate case and are governed by a constrained form of the more general Navier-Stokes equations, which we often call the Boundary Layer Equations. Only people that are irrelevant would dare say these boundary layers are irrelevant in the study of turbulence of fully developed boundary layers! Albeit, there has also been a change of variables to vorticity instead of velocity. 4. Spectral methods are by far one of the most efficient ways of solving DNS |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
-
Join Date: Oct 2021
Location: -
Posts: 139
Rep Power: 5  |
Quote:
Thanks for your sincere answer. Honestly I can't totally understand what do you mean as I'm a newbie of turbulence field. So I want to get some recommendation of useful materials to study for understanding what do you mean. 1. I don't know periodic boundary condition well. All that I know about periodic boundary condition is exerting flow at outlet into inlet. But I don't know mathematical definition exactly. So at first I think I have to study periodic boundary condition first. I think after studying periodic boundary condition, then I have to study the meaning of mean pressure gradient. For that time, I want to know which materials would be useful to study mean pressure gradient and link my knowledge of periodic boundary condition to mean pressure gradient.  Materials for studying mean pressure gradient Materials for studying mean pressure gradient* If it is possible to let me know materials for periodic boundary condition, I want to know that also. 2 & 3. Now that you mention it, I have to study boundary layer equation before starting derivation of equation 3 and 4. All that I know about boundary layer equation is only Blasius boundary layer equation(laminar boundary layer equation). So at first, I'm wondering whether boundary equation you mentioned is Blasius boundary layer equation or something others. If it is not Blasius boundary layer equation, I want to know the name of boundary layer equation that you told me to study it. After studying boundary layer equation, I would have to study derivation of equation 3 and 4. In addition, for doing that, I want to get recommendation of materials for derivation.  Materials for derviation of equation 3 and 4 Materials for derviation of equation 3 and 4* If it is possible to let me know materials for boundary layer equation, I want to know that also. Thanks for Reading |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
As the pressure gradient is concerned, you could find useful to read Sec.5.1 here https://www.researchgate.net/publica...ection_methods The numerical method proposed by Kim and Moin was one of the formulations for solving NSE. It is an alternative to the fractional methods. The SIMPLE method you studied is not suitable for time-dependent simulation at high accuracy as required for DNS/LES formulations. A good material to study turbulence is the textbook of Pope. |
|
|
|

|
|
|
|
|
#5 | |
|
Senior Member
-
Join Date: Oct 2021
Location: -
Posts: 139
Rep Power: 5  |
Quote:
Thanks for answering. By the way, is 'Turbulent Flow' by Pope treating detailed parts of DNS? I read some parts of his book before, but what I remember is physics of turbulence which would be usuful to post-process and overview of simulation if I remeber correctly. Is there any specialized material of DNS for newbie? Or Should I read reference paper from DNS part of 'Turbulent Flow' or review paper of DNS such as lower link? (https://www.researchgate.net/publica...lence_Research)  Reference from 'Turbulent Flow' or Reference from review paper or any other specialized material? Reference from 'Turbulent Flow' or Reference from review paper or any other specialized material?Thank you for Reading |
||
|
|

|
||
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
DNS means you solve the NSE without adding any turbulence model in unsteady and 3D (quasi-2D only for geophysical flows) using any numerical method but on a grid so fine to resolve all the turbulence scales. You need to know the physics of turbulence to understand if your DNS solution is physically acceptable. Pope is a good textbook where you can study. From the numerical perspective you can have a look to the section in the Ferziger et al. textbook. A lot of material about DNS appeared on JCP, JFM, PoF. You can find more references in my lectures about DNS/LES available on my page on ResearchGate. |
||
|
|

|
||
 |
| Tags |
| cfd, derivation, numerical method, turbulence |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Asking help on derivation of ALE differential form of momentum conservation equation | pfguo | Main CFD Forum | 10 | May 5, 2024 21:34 |
| Derivation of k-omega SST turbulence model. | dweaver123 | Main CFD Forum | 2 | August 7, 2020 13:12 |
| Call the parameter mut from the turbulence models to momentum equation | upuli | OpenFOAM Programming & Development | 0 | April 22, 2016 01:50 |
| Zero equation turbulence model gives better result?? | Sanyo | CFX | 10 | June 26, 2011 11:58 |
| Derivation of Momentum Equation in Integral Form | Demonwolf | Main CFD Forum | 2 | October 29, 2009 20:53 |