 |
|
|
[Sponsors] | |||||
Time derivative terms in RANS modeling equations |
 5Likes
5Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
K
Join Date: Oct 2022
Location: Madison, WI
Posts: 19
Rep Power: 4  |
Hello,
I am studying RANS closure models. In many of these models, for example the k-epsilon model, you will see time derivative terms. For instance the k equation starts with the term 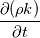 . But, in the RANS framework, the turbulent kinetic energy is defined as . But, in the RANS framework, the turbulent kinetic energy is defined as  Where the overline denotes the Reynolds operator, 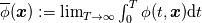 And 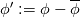 But clearly, this should mean that for any 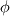 , that , that 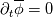 right? So why is there a time derivative in the k equation. right? So why is there a time derivative in the k equation.Also, what on EARTH is "unsteady RANS"? Isn't that a total oxymoron? |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
You are right, RANS equations, based on ergodicity hypothesis, says that all statistical averages converge to the same result. Thus, the time averaging produces a steady solution as well as an ensemble averaging. There is a lot of confusion when a time derivative is introduced somehow "artificially". What is denoted as unsteady RANS (URANS) has a debateble physical meaning if used for general flow problems and not only for specific ones. Have a look to this discussion: https://www.researchgate.net/post/UR...tUgCubNRviFeVq |
||
|
|

|
||
|
|
|
#3 |
|
Senior Member
|
However...
1) Reynolds himself introduced a wide variety of averages, including LES-like ones and the Favre one. I'm also pretty sure he wasn't the one that introduced the term RANS. Thus, I'm kind of convinced that whoever for the first time used RANS to refer to a time average was certainly superficial on the syntactic level. 2) Neglecting syntactic confusion and errors from the past, it is nowadays widely accepted by the relevant academic community that the most appropriate average to use in formalizations for both steady and unsteady flows is the ensemble one. As no actual average is ever performed in (U)RANS, the matter revolves about what your RHS is and what it implies with respect to the advancement in the LHS. Nothing of what is currently done in (U)RANS is specifically in favor or against this or that interpretation because, well, this is how little we understand about turbulence. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
On why unsteady RANS is not oxymoronic: the time-average operator is a Reynolds operator. The average of the time-average is what we often call the mean. But any statistical averaging (or filtering) method that is a Reynolds operator will result in a Reynolds average. Hence, there are many averaging operators that allows you to construct steady or unsteady reynolds averaged navier-stokes equations.
I highly recommend reading the work of Reynolds if you want to understand more: A. K. M. F. Hussain and W. C. Reynolds, “The mechanics of an organized wave in turbulent shear flow,” J. Fluid Mech. 41(02), 241–258 (1970). https://doi.org/10.1017/S0022112070000605 In short, RANS doesn't necessarily mean steady and unsteady RANS is redundant and should just be called RANS. However, due to the widespread misconception that RANS is steady, many people tend to write unsteady RANS when the context is needed. Because clearly, some people don't get it. |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
The real problem, as Paolo addressed, is that there is no Reynolds operator really applied on the equations other than for the case of the steady equations.
Any other possible argument about local time averaging or ensemble averaging turns to be never practically applied. The distinction between RANS and URANS is suitable, it means that the former is the only formulation having a distinct statistical averaging simply because the absence of time derivatives. When we call URANS something where the role of the variable is not statistical but more like a time-filtered variable, that is no longer a Reynolds operator. |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
I invite you to read the paper of Reynolds, specifically page 129
https://zenodo.org/record/1432102/files/article.pdf |
|
|
|

|
|
|
|
|
#7 |
|
Member
Youssef Hafez
Join Date: Dec 2022
Posts: 48
Rep Power: 4  |
I think the matter can be easily resolved if we consider different time scales for Reynolds averaging and for unsteady motion. For example, for Reynolds averaging the time scale could be so small (say in the order from 10^-3 to 10^-6 seconds) in which the average of the turbulent fluctuations could be considered constant so their time average is zero. In unsteady motion the time sale is significantly larger (say in the order of seconds or fraction of seconds) in which the variables could vary. To make it easy to visualize this situation, This looks like a stair-case function where within each stair step the turbulent variables are fluctuating up and down about a mean value with an average of zero. However, from one step to another the time average is different and this represents unsteady motion.
|
|
|
|

|
|
|
|
|
#8 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
No, the problem is not resolved simply in how considering that different time scales are involved but it is in how the presence of such unsteady feature is practically taken into account into the equations. I mean, do you see some finite-scale time-averaging operator really in action on the URANS equations? Of course the answer is no... the time derivative works on a function and what is this function would be established in a rigorous way only if the closure model express the type of averaging. For this reason only the steady RANS equations are well defined while the unsteady RANS has not (yet?) a solid theoretical framework. |
||
|
|

|
||
|
|
|
#9 |
|
New Member
K
Join Date: Oct 2022
Location: Madison, WI
Posts: 19
Rep Power: 4  |
Dr Hafez,
Thanks for this idea. Do you mean something like this? https://www.desmos.com/calculator/9dulfodgih As you can see, the small fluctuations, which have a frequency of 100, have been filtered out, but the larger fluctuations, which have a frequency of 1, remain in the filtered result. |
|
|
|

|
|
|
|
|
#10 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Again, there is a lot of confusion in these formulations. |
||
|
|

|
||
|
|
|
#11 | |
|
Senior Member
andy
Join Date: May 2009
Posts: 322
Rep Power: 18  |
Quote:
Consider performing a simulation with, say, a reciprocating motion imposed by a moving boundary on a time scale an order of magnitude or more slower than that of the energy containing turbulent motion. What term in the k turbulence equation would be required to account for this unsteady variation in time? Problems arise when unsteady motion that isn't turbulence starts to become quick enough to occur on the scale of the turbulent motion. In these circumstances one is forced to introduce a mechanism to separate the largest/slowest turbulence scales and the non-turbulent unsteady motion. An LES approach is the obvious way to do it these days but if the non-turbulent motion is coherent or periodic there are other options like ensemble averaging or something similar. |
||
|
|

|
||
|
|
|
#12 |
|
Member
Youssef Hafez
Join Date: Dec 2022
Posts: 48
Rep Power: 4  |
I agree with all the physical arguments presented by the previous writers. However, the issue we discuss here is mathematical in nature as we speak about the unsteady K transport equation or (k and epsilon equations). If the velocity field is unsteady, the modeling structure of the production terms in the k and epsilon equations are velocity dependent which means they have to be unsteady too. That means that k and epsilon variables themselves would be unsteady. So to account for this unsteady conditions time derivatives for k and epsilon are introduced which is just a mathematical necessity. This is similar to the fact that the pressure appearing in RANS is not the thermodynamic one but it is a mathematical constraint to force free divergence of the velocity field (this was addressed in another post by the respected writers here). So we have to differentiate between model equations that are mathematical in nature that have several approximations that we might like or dislike and some are not really perfectly physically based. I iterate here that the only logical explanation is that the time scale of unsteady motion is way much larger than the time scale of Reynolds averaging process. Of course no mention of the exact value of these time scales are stated but having different order of magnitude of these two time scales is well established.
|
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Mathematics is not something we can disregard just because one doesn't like or prefer only a physical explanation. One solves mathematical equations plus BCs. and that defines the final solution. In numerics you can assume the solution is an approximation of the "ideal" continuous solution but in the discussion in this thread the issue is that the ideal solution is never mathematically well defined in its meaning!
In the URANS equations any time derivative appears applied on a variable which meaning depends on all the other terms in the equations. The same happens in LES. I'll bet you if you are able to deduce the time averaging, ensemble averaging, spatial filtering or any type of mean if I just write down an equation. It could be URANS or LES, in no way the operator is really applied. This is because people use to commute the operators and the real application of a mean or filter operator vanishes. The only way one can distinguish the variables is by mathematics and physics, that is by looking into the closure model to see if a lenght or time scale is selected as well as by looking at the BCs. Otherwise, the correct approach is to never commute the operators and practically apply the mean operator on each term of the equations. Any other discussion in terms of the physics (k, eps or others) is full of flaws. URANS or LES we just have an unresolved variable in space and time. For this reason the well defined approach (the paper of Reynolds use the unsteady equations but clearly stated the mean to be well defined only for statistically steady flows) is the steady RANS. |
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
To further explain it... If it is a Reynolds operator, when you apply it to the Navier-Stokes equations you will arrive at the same Reynolds-Averaged Navier Stokes Equation. The Reynolds-Averaged Navier Stokes equations themselves, are just the navier-stokes equations except that the instantaneous transport variables are replaced by their Reynolds-Averaged counterparts. This is the property of a Reynolds operator that makes a Reynolds operator what it is. All Reynolds operators will give the same result, regardless of which operator you use. Additionally, for all RANS formulations, if you replace the Reynolds-averages by the instantaneous/molecular quantities, you get the original Navier Stokes back, i.e. you do a DNS.
Now you then hand your governing equation over to a linear solver (a computer) that solves the equations L{x}=0 and they are the same for all possible Reynolds averages. The computer has no way of knowing what type of Reynolds average x is, it just solves the linear system and gives the answer. The closure models you employ implicitly result in a solution that gives a particular x regardless of what you think x ought to be. Since all x's are equivalent and out of your control, you can apply Occam's razor rather and take it as being steady rather than trying to come up with an explanation to make them all fit. Because notice that the steady interpretation (almost) always works! The truly exceptional case is if you have some ungodly closure model that actually is unsteady. Such a model would likely solve the closure problem of turbulence and be near the realm of a turbulence law. Otherwise, as explained, the correct approach is to consider an actual temporal/spatial filtering and to do it without assuming that it is a commuting Reynolds operator and then you can easily say your filtered variables filter scales greater or less than such and such. But these governing equations we don't call RANS, we call them filtered Navier-Stokes. LES is an example. |
|
|
|

|
|
|
|
|
#15 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
I agree and, unfortunately, people seem not aware of what they are doing using URANS. There is still a lot of modern literature publishing results for statistically steady flows (no external forcing) claiming URANS captures the unsteadiness of the flow without understanding that they are performing a different simulation, more related to an unresolved DNS with a supplied wrong closure.
|
|
|
|

|
|
 |
| Tags |
| kepsilon model, rans |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Slow calculation time on CFD server | killian153 | Hardware | 4 | July 27, 2021 08:28 |
| Extrusion with OpenFoam problem No. Iterations 0 | Lord Kelvin | OpenFOAM Running, Solving & CFD | 8 | March 28, 2016 12:08 |
| Star cd es-ice solver error | ernarasimman | STAR-CD | 2 | September 12, 2014 01:01 |
| Moving mesh | Niklas Wikstrom (Wikstrom) | OpenFOAM Running, Solving & CFD | 122 | June 15, 2014 07:20 |
| Could anybody help me see this error and give help | liugx212 | OpenFOAM Running, Solving & CFD | 3 | January 4, 2006 19:07 |