[Ford Prefect]

Hey,


Is it possible/reasonable to use rational number instead of floats for CFD workloads?



Without using Google I would assume that the answer is NO, just based on looking at current CFD software as well as in standard textbooks.



If execution speed would be of similar order of magnitude then it seems to me that avoiding truncation errors would be a nice feature.


I have put together a simple test in Julia to benchmark rationals vs floats for the simple 1d heat equation. Unfortunately the results are not encouraging. Not sure if this is due to the matrix solver used by Julia or if it is connected to CPU instruction sets, or something else.


For larger meshes you may have to use BigInt in order to avoid overflow errors, since the size of the numerator/denominator can become quite large.



What do you think?

# Steady heat equation without sources. FDM discretization. 1D.
# Calculations use rational numbers vs floats

function rationalCFD(N)

    T = zeros(Rational{Int32},N) # BigInt may be needed to avoid overflow
    A = zeros(Rational{Int32},N,N) # Dense matrix used for this example
    b = zeros(Rational{Int32},N)

    b[1] = 100//1
    b[N] = 200//1

    A[1,1] = 1//1
    A[N,N] = 1//1

for i=2:N-1
        A[i,i] = 2//1
        A[i,i-1] = -1//1
        A[i,i+1] = -1//1
end

    T = A\b

#=     println("Output from rationalCFD")
    display(Float64.(T))
    println() =#

end

function floatCFD(N)

    T = zeros(Float64,N) 
    A = zeros(Float64,N,N) # Dense matrix used for this example
    b = zeros(Float64,N)

    b[1] = 100
    b[N] = 200

    A[1,1] = 1
    A[N,N] = 1

for i=2:N-1
        A[i,i] = 2
        A[i,i-1] = -1
        A[i,i+1] = -1
end

    T = A\b

#=     println("Output from floatCFD")
    display(T)
    println() =#
end

function test()

    N = 1000
rationalCFD(10) # first run include compilation so this is not included in timing

@time rationalCFD(N) # time the execution

floatCFD(10)

@time floatCFD(N)

end


test()

[LuckyTran]

Possible? Yes. Reasonable? Perhaps. Would anyone care of this? Probably not.

The speed is determined by the number of steps needed to execute operations, i.e. arithmetic.

Rational numbers are fundamentally the same class as floats, ordered pair representation of real numbers. With a float you store the mantissa and exponent and assume a base 10. You could change this base to some arbitrary number like pi, but most of the world likes base 10. With rational numbers, you store the numerator and denominator (your base) and assume an exponent of 1. You can also arbitrarily vary the exponent, but rational numbers by convention is exponent 1.

They are the same. In rational numbers you vary the base, in floats you vary the exponent. The difference between rational numbers versus floats is in the available dynamic range and what is the amount of the truncation error for various values over the range of the numbered pairs being stored.

And while I think there is some merit to your idea of "less truncation error," if the truncation error benefits of rational arithmetic exceeded floats we would be using it already for all arithmetic (not just CFD and heat equations) and we never would've settled on floats. There's more to life than numerical simulations. For example, what do you think the economic impact of truncation error is on conversions of national currencies or cryptocurrencies? There's real money at stake.

[Ford Prefect]

Thank you for your input LuckyTran.

While I could have searched for the answer, I think this question is a nice one for a warm summer evening. Food for thought can sometimes be a nice thing

Anyways, I think this is interesting, and after a quick search I now understand that integer precision is limited to (quote from Wiki)

"Integers from −253 to 253 (−9,007,199,254,740,992 to 9,007,199,254,740,992) can be exactly represented"

So you are correct that this would probably not be feasible for anything interesting in CFD seeing that the numerator and denominator can become quite large. Int32 and lower will not work for large domains and if I understand this correctly then Int64 will not be exactly represented if the number resulting from any operation is higher than 2^53.


I leave your questions about banking and money to someone else, although I would guess that they use Integers and when they need to round off something, then the bank always wins.

[JBeilke]

As long as you are doing +-*/ you can stay within RationalNumbers, use integer arithmetics and everything is fine. But a sqrt() or sin() forces you into FloatingPoint numbers.

There is a nice video, which also covers RationalNumbers:
https://www.youtube.com/watch?v=Nq2HkAYbG5o

[LuckyTran]

You can represent transcendental numbers using rational numbers to within the truncation error if you use rational number arithmetic. That's not the issue from a matter of principle. The issue is, the truncation error when you do this is generally not what we like.

Numbers don't need to be exactly represented (unless that is your goal), they only need to be represented up to machine precision. For example, in floats there is no exact representation for the addition of "zero."

Keep in mind all numbers that can be expressed in floating point representation are by definition rational numbers. That is, all floats are rational numbers. Again, they're categorically the same. The difference is do you vary the exponent or the base?

[FMDenaro]

Just my curiosity, what about software that use symbolic operation?
I often worked with maple using also rational nunbers, how they manage large integers?

[Ford Prefect]

Originally Posted by LuckyTran

You can represent transcendental numbers using rational numbers to within the truncation error if you use rational number arithmetic. That's not the issue from a matter of principle. The issue is, the truncation error when you do this is generally not what we like.

Numbers don't need to be exactly represented (unless that is your goal), they only need to be represented up to machine precision. For example, in floats there is no exact representation for the addition of "zero."

Keep in mind all numbers that can be expressed in floating point representation are by definition rational numbers. That is, all floats are rational numbers. Again, they're categorically the same. The difference is do you vary the exponent or the base?

I can share my initial thoughts, although I now realize that they were somewhat flawed. Perhaps that will answer some of the questions.


In CFD my experience is that round-off errors are important in single precision, but perhaps not in double precision. On GPUs, single precision operations are much much faster, so if we can use single precision without compromising accuracy then that would be a good thing. And lastly, as I said in my second sentence in the original post, I do understand that it is not that easy, since then everyone would use it. But I was still curious about this question so.


For a rational number, say 2/3, this will be exactly represented if using rationals, but if using floats it will be rounded at machine precision.


Any rational number up to about 2^53/2^53 will be exact (for 64 bit integers), if 11 bits are used for the exponent (which is one).



So a simple example (there may be better ones):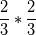






will give a round-off error. So if using 32 bits this will be represented as: 0.444444477558136, and with 64 bits it will be represented as 0.4444444444444444.


We can use any precision rational to get the 64 bit result (in my example I use an 8 bit integer).

julia> Float64(Float32(2/3)*Float32(2/3)) 

0.444444477558136  


julia> Float64(Float64(2/3)*Float64(2/3)) 

0.4444444444444444  


julia> Float64(Rational{Int8}(2//3)*Rational{Int8}(2//3)) 

0.4444444444444444

Originally Posted by FMDenaro

Just my curiosity, what about software that use symbolic operation?
I often worked with maple using also rational nunbers, how they manage large integers?

I do not know, but arbitrary precision exists in Julia. Perhaps something similar?


https://docs.julialang.org/en/v1/man...ion-Arithmetic

[LuckyTran]

Symbolic manipulators abuse that you have higher level software control and are not performing low-level executions on hardware and don't have to strictly obey those rulesets for storing numbers in memory. In software you use variable length data vectors as a memory structure. These vectors can be long and use up any and all capacity available. Afterwards you can still emulate the same operations (equivalent to the instruction set minus the rounding to preserve exact precision), they'll just be very slow to execute.


At the hardware level you are restricted to performing arithmetic on two binary64 numbers just as an example. At the software level I can write a program that does all the same things but for larger memory sizes as long as I manage and keep track of the sizes of each and every one of my vectors.

[LuckyTran]

Again, computations are not about storing cherry picked numbers with exact accuracy. It's about taking two or more inputs and doing math on them! If you restrict all your dimensioned values to being purely rational numbers, then you are doing integer arithmetic on the space of rational numbers and not rational arithmetic on the space of real numbers. Maybe you are okay with this..

Originally Posted by Ford Prefect

Any rational number up to about 2^53/2^53 will be exact (for 64 bit integers), if 11 bits are used for the exponent (which is one).

You don't need to expend 11 bits on an unused exponent in the same way that floats don't waste bits to remind everyone that the base is 10. With 64 bits, and if you reserve 1 for the sign then you have 31 and 32 bits remaining for the numerator or denominator. That means your rational numbers covers a span of 2^31/2^31 ish

With 8 bits, and generously giving you 3 bits in the numerator and 4 in the denominator means you have a machine precision of 1/15. You do a great job of storing 2/3 exactly except you can't distinguish it from any number between 9/15 thru 11/15. Obviously you're going to need a lot more than 8 bits to get any type of accuracy. That is, you need to consider that 2/3 has an uncertainty of +/- 1/30. Because how do you know the length of a particular edge is exactly 2/3 to begin with? That's the error that you need to propagate through your analysis.

[Ford Prefect]

Originally Posted by LuckyTran

Again, computations are not about storing cherry picked numbers with exact accuracy. It's about taking two or more inputs and doing math on them! If you restrict all your dimensioned values to being purely rational numbers, then you are doing integer arithmetic on the space of rational numbers and not rational arithmetic on the space of real numbers. Maybe you are okay with this..

I am not sure, that is why I asked. My initial example was with 32 bit rationals and that works well except for abysmal execution speed.

Originally Posted by LuckyTran

You don't need to expend 11 bits on an unused exponent in the same way that floats don't waste bits to remind everyone that the base is 10. With 64 bits, and if you reserve 1 for the sign then you have 31 and 32 bits remaining for the numerator or denominator. That means your rational numbers covers a span of 2^31/2^31 ish

Sounds reasonable, I just made an assumption based from the Wiki page that since a 64 bit integer can be represented exactly with only 2^53, that we still had to pay the tax for the 11 bit exponent.

Originally Posted by LuckyTran

With 8 bits, and generously giving you 3 bits in the numerator and 4 in the denominator means you have a machine precision of 1/15. You do a great job of storing 2/3 exactly except you can't distinguish it from any number between 9/15 thru 11/15. Obviously you're going to need a lot more than 8 bits to get any type of accuracy. That is, you need to consider that 2/3 has an uncertainty of +/- 1/30. Because how do you know the length of a particular edge is exactly 2/3 to begin with? That's the error that you need to propagate through your analysis.

Sorry I do not understand this. In Julia an 8 bit Rational is (2^7-1)/(2^7-1), so any rational number up to 127/127 would be OK. Obviously this is not something we can use in CFD , but as my original example shows, it is possible to use Int32 for the test case (and Int16 for say N=10). I do agree that this is probably not feasible and if we are forced to use BigInt (arbitrary precision) then all hope of execution speed goes out the window.


As long as we can stay within Int32 for the numerator and denominator then would it not be possible to run this efficiently on single precision hardware?


The question about uncertainty in initial data and/or boundary conditions is obviously important. However, for this discussion it may not be that important, since we would get the same end-result. Just that single precision calculations could be obtained much faster if it would work.

[sbaffini]

Just as a side note, in banking and economics they use https://en.m.wikipedia.org/wiki/Fixed-point_arithmetic

[LuckyTran]

Using 8 bits for the numerator and 8 bits for the denominator, that is a 16 bit rational, not an 8 bit rational. Actually you can use unsigned integers for the numerator and denominator and use one bit (and not two) to store the sign of the rational number at the end. It's up to your whether you give this bit to the numerator or denominator but your range for hypothetical 16 bit rational would be more like (0-127)/(1-256), but it would be 16 bits, not 8. Alternatively you can use 15 bits to represent a range of 127/128. So yes, a 64 bit rational would mean a 32 bit integer for the numerator and 32 bit integer for the denominator, +/- 1 bit.

You are right we don't actually need to go through a detailed uncertainty analysis as long as you understand that if a is an actual real quantity we want to represent and p and q are our two integers for our rational number, then a~p/q, i.e. not necessarily equal, but results in the best rational representation of a, up to machine precision. It's not about exactness, so we can also stop talking about that. The number of exactly represent-able numbers in your number system is the number of rational numbers in your number system. That much should be obvious. Floats have the same properties, they're just not integers but decimals.

In general, arithmetic operations on floating points are operations on rational numbers. The benefit that floats have is certain specific operations can be accelerated. For floats you can add powers of 2 to the mantissa very quickly by simply flipping the binary in memory without actually adding doing the math. You can multiply or divide by 10 very quickly by just just incrementing the exponent.

Rational numbers also have similar properties but with a quirky pattern. Using again p for the numerator and q for the denominator you can add fractions of q very quickly by incrementing the numerator (equivalent to powers of 2 in floats except that you now add powers of q). You can multiply and divide by integers quickly by incrementing/decrementing the denominator. If I want to divide a number by 3, I just add 3 to the denominator in memory but without it ever going to an ALU. If I want to divide by 3, then I subtract 3 from the denominator. 3 in binary is 0....011. Adding or subtracting them in memory means I go straight to the last two bits and flip them. I don't actually add/subtract 3 to q, I just modify the last two bits.

These are the fundamentals and how well you abuse these specific properties in a general setting determines how fast the calculation ultimately is. Outside of these memory abuse tricks, most other calculations are the same for floats versus rationals because floats are rationals. A notable instruction set used for acceleration is the FMA.

GPU's can do FP32 operations much faster than FP64 operations because their hardware doesn't support fully all operations at the FP64 level that they do at 32 bits. For the unsupported operations.... they emulate it! If you compare the performance gains of FP32 to FP16 on a gpu, you'll find that they scale much better and more logically than the performance loss of going from FP32 to FP64. In the future that could change if gpu manufacturers rethink their hardware strategy. In a dystopian future, if CPU manufactures decide to cut costs and remove hardware for performing FP64 operations then that could also introduce the same bottleneck to cpu calculations. Or maybe it doesn't happen at the FP64 level but this issue arises when FP128 operations are implemented non-uniformly for CPUs and GPUs.