 |
|
|
[Sponsors] | |||||
Numerical implementation of Boundary conditions in fractional step method |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Join Date: Feb 2011
Posts: 41
Rep Power: 15  |
Hello,
I know there are a lot of debates on the choice of the boundary conditions in the fractional step method. I'm reading Kim and Moin's 1985 JCP paper. I can understand most of it but have some difficulty in understanding the boundary conditions. May I ask the following question? In their paper, see the screenshot below, where they used Taylor series to get boundary conditions for the intermediate velocities, it requires to evaluate the derivative of phi on the boundary. In staggered grid, phi is defined on the center of cells. Does it mean that we should use one-sided finite difference method to get the derivatives of phi on the boundaries (basically extrapolation)? Thanks. Screenshot 2021-11-16 at 08.27.52.jpg |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Actually no. The derivative is evaluated at the previous time step, thus you have already solved the Poisson problem with the Neumann BCs and your d(phi)/dn is already computed. However, be carefull that the second order Taylor series does not imply that the BCs produces a second order accurate truncation error, you can see that it is a firts order accurate BC. |
||
|
|

|
||
|
|
|
#3 | |
|
Member
Join Date: Feb 2011
Posts: 41
Rep Power: 15  |
Quote:
I'm not sure if I understand you correctly. In staggered grid, the pressure is defined at the cell center. For uniform grid, the boundary is half-cell-distance away from the first cell center. Even for the pressure gradient from the last time step, we still need to extrapolate in space to get the pressure gradient at the boundary. Am I right? |
||
|
|

|
||
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
No. You have already the value of the derivative on the boundary, you do not need to discretize. The expression you used in the previous time step is n.(v* - vn)/dt, v* being the intermediate value of the previous time step. This is the Neumann BCs used for solving the pressure equation at tn. To better understand, consider the intermediate velocity at the time step n+1 and that at the time step n. |
||
|
|

|
||
|
|
|
#5 | |
|
Member
Join Date: Feb 2011
Posts: 41
Rep Power: 15  |
Quote:
I have written down the two steps for v velocity as you suggested (with the AB2 and CN method). Please be more specific on how to understand the issue with 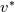 and and 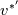 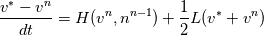 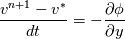 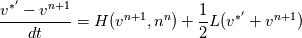 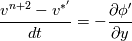
|
||
|
|

|
||
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
The paper of Kim & Moin is exactly what I am referring. You need to consider the whole procedure. That is to compute the intermediate BCs for v* at time tn+1 you need to consider the computation of the pressure at time tn.
At the time step tn you compute the pressure problem Div Grad phi = (1/dt) Div v* with the Neumann BC n.Grad phi = (1/dt) n.(v* -v) That is you have the pressure computed in the cell center but also the evaluation of the derivatives on the faces lying on the boundary (RHS). If you wnat, you can see that like using ghost point and computing the central derivative at second order of accuracy. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Have also a look to these papers
https://www.researchgate.net/publica...ection_methods https://www.researchgate.net/publica...v8onk7-JA9ssEA |
|
|
|

|
|
|
|
|
#8 | |
|
Member
Join Date: Feb 2011
Posts: 41
Rep Power: 15  |
Quote:
Screenshot 2021-11-16 at 19.17.54.jpg |
||
|
|

|
||
|
|
|
#9 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
In fact, for a staggered grid the tangential components is posed badly ... I highlighted this problem in the paper and the need to have more accurate intermediate BCs. Clearly, you could think u* located at a ghost node or considering a different derivative for the diffusive term along y in such a way to have the last cells close to the boundaries of half size and u* located exactly on the boundary. Then you have to construct the tangential derivative d phi/dt along the boundary. |
||
|
|

|
||
|
|
|
#10 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Note that the red arrows must be defined also on top and bottom boundaries |
||
|
|

|
||
|
|
|
#11 | |
|
Member
Join Date: Feb 2011
Posts: 41
Rep Power: 15  |
Quote:
Because I impose no-slip boundary conditions for the v velocity (red arrows), I don't have to include these boundary grid points in the solution process, right? I already know their values. |
||
|
|

|
||
|
|
|
#12 |
|
Senior Member
|
The Taylor series is used to eventually obtain the dp/dn bc for the pressure, which is needed on the boundary faces of the pressure cells. But the resulting dp/dn for a given face is, in fact, only dependent from the velocity known on that very face, the normal to the face velocity.
Also, that very velocity (the normal to the face), also happens to appear in the source term for the neighbor cell in the pressure equation so, in the end, they cancel each other out. |
|
|
|

|
|
|
|
|
#13 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
No, you are wrong. The intermediate velocity on the wall is not the physical velocity! The formula proposed by Kim and Moin is valid everywhere and you have to use for both u* and v* along the walls. |
||
|
|

|
||
|
|
|
#14 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
That's correct but the devil is in the details... using the implicit formulation (CN) requires to prescribe the Taylor expansion also for the tangential velocity and the tangential pressure gradient must be evaluated. And there ... is the devil. All that is in the approximation produces the so-called numerical boundary layer. And if the decomposition is not orthogonal, the error in the pressure enters into the tangential velocity and viceversa. |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Table bounds warnings at: END OF TIME STEP | CFXer | CFX | 4 | July 17, 2020 00:44 |
| UDF for Automatic Solution Initialization for previous case data file | gartz89 | Fluent UDF and Scheme Programming | 6 | March 30, 2020 08:38 |
| Error - Solar absorber - Solar Thermal Radiation | MichaelK | CFX | 12 | September 1, 2016 06:15 |
| Problem with SIMPLEC-like finite volume channel flow boundary conditions | ghobold | Main CFD Forum | 3 | June 15, 2015 12:14 |
| Water subcooled boiling | Attesz | CFX | 7 | January 5, 2013 04:32 |