 |
|
|
[Sponsors] | |||||
[LES] Dynamic Smagorinsky coefficient: scalar or a tensor? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Hello,
First of all, Sorry if the question is amateur I'm am very noob in Einstien notation! As you know, SGS stresses tensor is  . .Also, Germano identity is a tensor 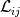 . .Then the coefficient of dynamic Smagorinsky is calculated by 2 tensors (with or without Lily's correction): 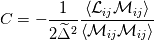 While 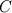 does not have an index, it seems that it's a scalar! I really don't understand how can it be possible that the divide of two tensors is a scalar! does not have an index, it seems that it's a scalar! I really don't understand how can it be possible that the divide of two tensors is a scalar!This means: (suppose for example we have a 2d case) 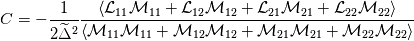 My question is, why it is not calculated like this: 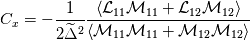 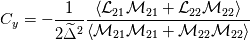 Then we can have 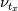 and and 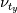 which can be used in which can be used in  and and 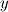 momentum equations. momentum equations.
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
The fact that the eddy viscosity is a scalar function or a tensor function depends on the chosen functional relation you use for the model. It is not a result of the Germano identity and the consequent contraction.
Indeed, there are anisotropic models in tensor form, see Sagaut. |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Quote:
My question was a little mathematical: How can it be possible to divide two tensors and the result is a scalar? 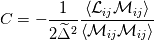 The numerator is the product of two tensors and the denomerator is the same. But the left hand side is a scalar. |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
You have to consider the double scalar product between the two tensors, it is a scalar function
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
||
|
|

|
|
 |
| Tags |
| dynamic smagorinsky, les |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Creating a transient .case file | scro1022 | EnSight | 0 | November 27, 2020 11:11 |
| [General] Problem with reading in multiple grouped Ensight .case files into paraview | scro1022 | ParaView | 0 | November 27, 2020 09:00 |
| Updating the turbulent schmidt number in dynamic smagorinsky model | pvpnrao | OpenFOAM Running, Solving & CFD | 3 | November 6, 2020 04:52 |
| is internalField(U) equivalent to zeroGradient? | immortality | OpenFOAM Running, Solving & CFD | 7 | March 29, 2013 02:27 |
| Automotive test case | vinz | OpenFOAM Running, Solving & CFD | 98 | October 27, 2008 09:43 |