[Moreza7]

Hello,

As you know, the small scales are in near-wall regions where the viscosity effect is dominant there.

Also, by Kolmogorov's hypothesis, small scales are isotropic. But in all of the turbulent flow books, it is mentioned that near-boundary scales are anisotropic.

Do these two claims conflict?

Finally, the near-wall scales are isotropic or anisotropic?

Best regards

[FMDenaro]

Originally Posted by Moreza7

Hello,

As you know, the small scales are in near-wall regions where the viscosity effect is dominant there.

Also, by Kolmogorov's hypothesis, small scales are isotropic. But in all of the turbulent flow books, it is mentioned that near-boundary scales are anisotropic.

Do these two claims conflict?

Finally, the near-wall scales are isotropic or anisotropic?

Best regards

Your error is that small vortical structures are not due to wall confinement. They are isotropic for a large distance from the wall at high Re flows

[sbaffini]

Near wall scales are anisotropic. To see this consider that energy comes from the streamwise motion only and that wall normal fluctuations are damped near the wall... well, because of the wall (continuity, actually). Also, if you look at the spectra of the velocities near a wall, you will see more energy at small scales than at the large ones.

The Kolmogorov picture assumes homogeneous and isotropic turbulence, so it is not applicable near a wall. But if you look at the RMS of the velocity fluctuations going away from a wall, you will see that far away they will tend to be equal to each other (the turbulence is isotropic away from the wall).

[Moreza7]

Thanks a lot.

So, what I understood is that Kolmogorov's hypothesis is for isotropic turbulence where we can not specify a mean flow in a specific direction.

Kolmogorov's hypothesis is not valid for near wall regions.

And the reason of that the reynolds shear stress is maximum in the buffer layer in channel flow, is becuase of the strong anisotropy there.

And even the walls damp the energy and tutbulence, they are also the source of turbulence.

[Moreza7]

Originally Posted by sbaffini

Near wall scales are anisotropic. To see this consider that energy comes from the streamwise motion only and that wall normal fluctuations are damped near the wall... well, because of the wall (continuity, actually). Also, if you look at the spectra of the velocities near a wall, you will see more energy at small scales than at the large ones.

The Kolmogorov picture assumes homogeneous and isotropic turbulence, so it is not applicable near a wall. But if you look at the RMS of the velocity fluctuations going away from a wall, you will see that far away they will tend to be equal to each other (the turbulence is isotropic away from the wall).

I found something new!

1- As you can see in this picture the shear reynolds stresses which are a criteria to determine the isotropy, will tend to zero in the middle of a turbulent duct flow.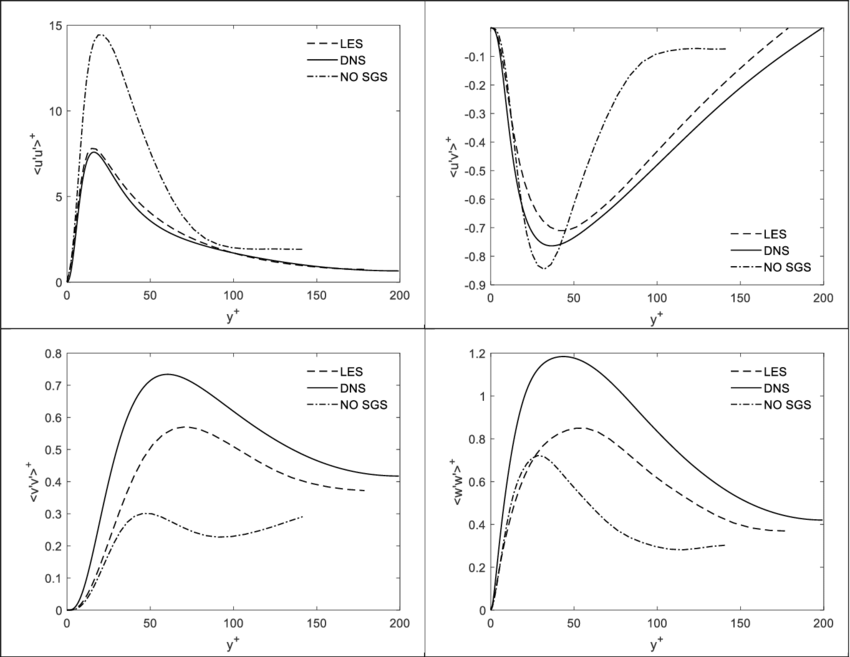



As you know, away from the wall, the turbulent structures get bigger and bigger, and they are certainly bigger than Kolmogorov's scales, then by Kolmogorov's hypothesis, they must become more anisotropic, but as you said(and as it is visible in the plots) they will become more isotropic instead of anisotropic!
It's wierd that smaller scales near the wall are more anisotropic than large scales away from the wall. [I know the shear is less away from the wall, but also the scales are bigger]
Does it conflict with Kolmogorov's hypothesis about the anisotropic structure of large scales?

2- Someone told me that there is no isotropy or homogeneity condition in Kolmogorov's hypothesis it's about all ofthe turbulent flows, not only homogenous isotropic turbulent flows.
He said that the Kolmogoorv's scals are very very small and located very very close to the wall where the shear reynolds stresses are close to zero and then it's hypothesis is not violated.