 |
|
|
[Sponsors] | |||||
Finite volume method for incompressible & compressible flow |
 13Likes
13Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
|
Greetings,
In Ferziger's book, for FVM, no matter what kind of interpolation scheme they discuss (in Chap.4.4, e.g., CDS, UDS, QUICK, etc), the values on cell faces are unique (if I understand it correctly): i.e., there are no left & right states as in those cases where methods like Riemann solver or flux-vector splitting are used. The latter appears to me that are majorly used in gasdynamics, namely for convection-dominated problems, high-speed flows, or hyperbolic equations. So, is it correct to say that the approach in Ferziger's book is more suitable for incompresssible flows (or low-speed flows, or for parabolic/elliptic equations), whereas methods discussed in, e.g., the book by LeVeque or Toro's book, are for high-speed/compressible flows (or hyperbolic equations)? Or, is it because what Ferziger presented in Chap.4 is for linear equations, thus no left & right states will show up? But what about when actually solving incompressible NS equations? |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Sayan Bhattacharjee
Join Date: Mar 2020
Posts: 495
Rep Power: 8  |
Quote:
Versteeg's book also focuses mostly on incompressible flows. Initially I thought it was a problem when I was trying to write my own compressible solvers and couldn't find the relevant information in the book.I only wrote compressible Euler solvers (as I only like supersonic and hypersonic flows), so I might not have the full knowledge to answer your question. But in my own case, addition of Van-Leer flux / Roe flux to the euler solver wasn't as difficult I thought it would be. I think that numerical solutions of the RIemann problem should be handled in a separate book as it is a special topic, and more focus should be given on the explanation of the FVM discretization (in 1D,2D,3D) in any entry level CFD books. Understanding the discretization, and having worked out examples in the book helps out a lot more than addition of an advanced topic. It is expected that the student would study different books when they want to understand the advanced topics.  Edit : Also it looks like I got the "Senior Member" badge. Anyways, time to celebrate : https://youtu.be/gu3KzCWoons 
|
||
|
|

|
||
|
|
|
#3 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
I think there is some confusion in intepreting the general idea of FVM. The unicity of the flux function on a face of a FV is a requirement for any FV method, no matter about solving linear problems, incompressible or compressible flows.
For example, consider a linear problem, the time advancement in FVM evaluates the cell-averaged variable, therefore each cell will have its own value. The face between two cells has right and left states and the flux is univocally determined on the face. That can be done using the Riemann problem but also by introducing some specific flux reconstruction method, as in QUICK, QUICKEST and many others. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
|
For any cell centered FV method, for each face which is not on the boundary (but, philosophically, we might claim even for them) there are two states, those associated to the two sides of the face.
This is independent from the order to which these states are reconstructed. Now, an upwind scheme will necessarily involve choosing one of those states using characteristics, even for scalar transport trough incompressible flows. But even central schemes actually build face values from those states. What makes the actual difference is that compressible schemes determine the fluxes all together, while incompressible ones split this in determining the mass flux plus the other ones, one by one. Once you know the mass flux, for the other fluxes the problem is necessarily reduced to determining the face value, but the two states on the sides of the face are still there and you actually use them to determine the face value |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Forget to add that one distinction is due to the presence of a singularity (i.e., shock wave) in a cell. In such a case, the reconstruction of the flux is theoretically possible from the averaged variables but not from the pointwise variable in the cell.
However, I know that a student has some difficulty in managing this topic, I suggest to read and pose some specific questions from the equations. |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,291
Rep Power: 35   |
You can mix things too though. In wildkatze you can also chose Roe as flux scheme while still solving pressure equation the way Prof Peric's book describe.
I was even using HLLC scheme in pressure based solver just last night on high speed cavitation benchmark in Wildkatze solver (scheme will be available from next release). Once you have flux, you can calculate the variable flux as (flux * var_face) how so ever you like. This flux is usually = velocity * rho * area + dissipation flux . Here for dissipation flux one can chose Rhie and Chow ( Prof Peric's book) or Roe, HLLC etc scheme as in gasdynamics could be used. |
|
|
|

|
|
|
|
|
#7 | |
|
Senior Member
|
Quote:
But based on Ferziger's book, seems like they never mention anything about this two-states situation. Also, they didn't introduce any numerical fluxes (if I am not missing anything); so what's the typical way of computing fluxes from these two states when solving incompressible flow? |
||
|
|

|
||
|
|
|
#8 | |
|
Senior Member
|
Quote:
|
||
|
|

|
||
|
|
|
#9 | |
|
Senior Member
|
Quote:
BTW, isn't QUICK just an interpolation scheme for reconstruction of face values? |
||
|
|

|
||
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
In the Sec.4.4 of the Ferziger's book you see some of the possible flux reconstructions, but you should be aware that:
1) the examples are for linear problems 2) it is assumed that the surface integral is discretized by the mean value formula If you read the Leonard's paper about the QUICK/QUICKEST methods you will get more details. However, Riemann problems are never explicitly explained in that book, you should consider the Leveque's textbook. It can be shown for example that a first order upwind is actually a way to solve the Riemann problem. Generally, the difference in the approaches is due to the fact for incompressible flows (divergence-free velocity) the variables are assumed pointwise continuous while appearence of singularity is possible in compressible flows. In more technical words, from the exact integral equation you have an averaged variable f_av=1/|V| Int f dV and the flux F(f). The two approaches can be seen as a closure relation in the form either f_av(f) or f(f_av). |
|
|
|

|
|
|
|
|
#11 | ||
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,291
Rep Power: 35   |
Quote:
They do because without numerical fluxes you can't write working finite volume flow solver. Quote:
Your issue as I understand here is that the book you are following does not do the things the way you are used to and you are finding it hard to give them a chance and read what they have to say. Put aside the two state concept for this book because here they discuss pressure based solver mainly used for incompressible flow. Though the book also mentions high speed flow related modifications to the fluxes too. |
|||
|
|

|
|||
|
|
|
#12 | |
|
Senior Member
|
Quote:
Could you briefly introduce some of the numerical fluxes that are commonly used in incompressible solver? |
||
|
|

|
||
|
|
|
#13 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,291
Rep Power: 35   |
Quote:
Still in nutshell: 1. As metioned in my first post think two things (a) flux (b) variables to be transported at the control volume face. 2. Flux is flux due to velocity (rho Velocity Area) and flux due to dissipation. 3. In the book you are following Rhie and Chow flux is used (the section i mentioned). 4. In density based solver flux is by looking at the state vectors from left and from right based on speed of sound. Now one important source of confusion is that in density based solver when the variables are iterpolated to the face there is a contribution to them due to dissipation too. While in the pressure based solvers we do not have that. This is why you do not see the left and right state vectors mentioned in the book. While in all the density based literature you see this. Another important thing that no book or no paper says is that you do not really need dissipation in variables at the face center, the dissipation in flux is good enough. (as happens in pressure based solvers). Using this idea one can actually mix the formulations , that is use the flux with dissipation from density based solver and use in formulation of pressure based solver. That is replace Rhie and Chow flux to AUSM or Roe or HLLC etc schemes. Why would you want to do so? The reason to do such thing is that the dissipation based on state vector is not timestep dependent but Rhie and Chow dissipation is. So when timestep size go small Rhie and Chow based solvers de-couple. |
||
|
|

|
||
|
|
|
#14 | |
|
Senior Member
|
Quote:
Anyway, really appreciate it! It's really helpful! |
||
|
|

|
||
|
|
|
#15 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,291
Rep Power: 35   |
Quote:
limiters come in play when you interpolate the variable to the face using the gradients. For example you can say your scheme is first order if the values at face is just cell center value from left/right. Second order would be when you have the value at face = value_cell + limiter * grad (var) . deltaR Based on these interpolated values you can calculate various things like flux or variable flux ( var_face * flux ) etc etc. The schemes that you usually hear ( upwind, second order upwind, bounded central, MUSCL , QUICK etc etc) are basically how using limiters and gradients you construct the values of variables at face. Last edited by arjun; January 5, 2021 at 06:02. |
||
|
|

|
||
|
|
|
#16 |
|
Senior Member
|
As a trivial example to clarify things, consider any order upwind for incompressible solvers. Assume we are transporting scalar
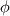 (can be any velocity component, temperature, etc.) with a precomputed mass flux (can be any velocity component, temperature, etc.) with a precomputed mass flux 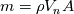 , where , where 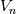 is not simply an interpolated velocity on the face, but one that actually satisfies your continuity equation on the cell (not really relevant for the discussion, but still). is not simply an interpolated velocity on the face, but one that actually satisfies your continuity equation on the cell (not really relevant for the discussion, but still).Now, for a given face 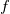 , considering that its mass flux is already given (i.e., , considering that its mass flux is already given (i.e., 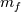 ), the convective flux of scalar ), the convective flux of scalar 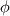 will have to be will have to be 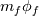 . How is this . How is this 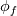 computed for an upwind scheme? As follows (actually this is the full flux formula, but you get the point): computed for an upwind scheme? As follows (actually this is the full flux formula, but you get the point):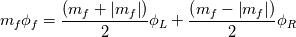 where 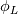 and and 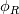 are the states on the two sides of the face (whatever is the order at which they are reconstructed), with the normal to the face assumed positive when going from L to R. are the states on the two sides of the face (whatever is the order at which they are reconstructed), with the normal to the face assumed positive when going from L to R.It should be clear now where those states enter the picture. If you consider first order upwind, I think, there should be no confusion, L and R just refer to the cell values on the two sides of the face. For HO reconstruction, I guess, your confusion might come from the fact that examples are typically for structured grids and those states are directly written in terms of additional cell values and everything is put together in one formula. But the formulation above is the actual one valid for any order and grid topology. As a side note, if you are using a density based solver with additional transported scalars (say, turbulence variables), the flux component from the continuity equation will directly give you the 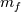 above to be used with the additional scalars. above to be used with the additional scalars.
|
|
|
|

|
|
|
|
|
#17 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
|
|
|
|

|
|
 |
| Tags |
| finite volume method, interpolationschemes |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Issues on the simulation of high-speed compressible flow within turbomachinery | dowlee | OpenFOAM Running, Solving & CFD | 11 | August 6, 2021 07:40 |
| References for Vertex Based Finite Volume Method | alibaig1991 | Main CFD Forum | 3 | May 25, 2018 19:20 |
| Mesh; wall function for element based finite volume method | sheaker | CFX | 2 | January 25, 2018 18:36 |
| Problem of simulating of small droplet with radius of 2mm | liguifan | OpenFOAM Running, Solving & CFD | 5 | June 3, 2014 03:53 |
| tidal flow simulation using finite volume method | Jason Qiu | Main CFD Forum | 0 | October 20, 2002 03:34 |