 |
|
|
[Sponsors] | |||||
Why the differential sequence switch at the first term of viscous shearing of N-S eq |
 10Likes
10Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Lee
Join Date: Nov 2020
Location: Taoyuan
Posts: 3
Rep Power: 6  |
Hello Everyone, I am a student to look for reasonable explanation to answer the doubt in my mind. Thank you all!
In the attached picture of Curric's text book, he didn't explain why he just switch the differential sequence partial Xi and partial Xj to get the first term of viscous shear term eliminated again by incompressible in order to have the neat Laplacian term to solve the problem with better chance. I know there is Fubuni's theorem in triple integral. I know continuum (continuity) is the base assumption of fluid dynamics. However, I am wondering if I can always do this kind of switch in fluid dynamics????????   Can anyone help? Thanks again! TommyWind |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Gerry Kan
Join Date: May 2016
Posts: 376
Rep Power: 11  |
Dear TommyWind:
This is a subtle point in using tensor notation. You can switch tensor indices in any way deemed convenient if it still retains the summation that it is meant to represent. As an example: While I was deriving some term in a turbulence model, I ended up getting a term which looked like this  Each of these two terms expand to the same expression (I will let you do this if you need some convincing). So you can simply collect them by switching the 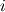 and and 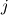 indices in the second term: indices in the second term: Hope that helps, Gerry. Last edited by Gerry Kan; November 13, 2020 at 06:03. |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
In the incompressible flow model, the continuity equation is simply dui/dxi=0. Use this divergence-free constraint in rewriting the term Div(2mu*S) where S is the symmetric part of the velocity gradient with zero trace. |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
|
Not sure who this Curric is, he surely is a good guy but, I must admit that this is one of the most appalling presentations of this matter I have ever seen so far.
For your mental sanity, I suggest you to switch to some more common reference. |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Lee
Join Date: Nov 2020
Location: Taoyuan
Posts: 3
Rep Power: 6  |
Dear Gerry,
Thanks a lot for your explanation. Will it explain your example when the matrix (of two tensors) is symmetry? Quote You can switch tensor indices in any way you deemed convenient if "it still retains the summation" that it is meant to represent. End of Quote The key point is you have evidence or proof that it still retains the summation. That means we have to prove sock first and shoe second is equal to shoe first and sock second in this case. In your example symmetry works, but not for my question. Otherwise, they are all eliminated by incompressible. The changing of partial differential sequences are always some physics meaning behind in fluid. But, I think I just found the reason when I go back to the definition of τ_ij. τ_ij = μ ( ∇V_i + ∇V_i^t ) therefore symmetry τ_12 = ∂/∂x(μ(∂u/∂y+∂v/∂x)) = τ_21 = ∂/∂y(μ(∂v/∂x+∂u/∂y)) Should I make any mislead or mistake, please let me know. P.S. I will study my turbulence flow next semester. By the way, what kind math tool do you use here? Thank you Gerry! All the best, TommyWind |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Gerry Kan
Join Date: May 2016
Posts: 376
Rep Power: 11  |
Dear TommyWind:
To be honest I have not thought about symmetry, but this is an interesting point. In the Curric case, there is a switch in indices in the differential, that is:  I believe your question hinges on this. If this is not correct please let me know. Going back to the above term, this is effectively saying (in 2D) for a fixed 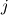 , say , say  (to be in line with the Curric convention, where each equation is fixed at (to be in line with the Curric convention, where each equation is fixed at 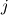 instead of instead of 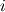 ): ): The only thing that "symmetry" would be brought in question is whether  There is where I am not 100% certain. I believe there are rare special cases, from a mathematical point of view, where this might not be the case. However, for most naturally occurring phenomena the differential order can be regarded as interchangeable. I am not sure if this answers your question, though. But please keep in mind that index notation is a shorthand, and is not an implicit indicator of tensor symmetry. Gerry. P.S. - You can enter Latex commands directly in the forum posts using the math formatting tags. For instance: Code:
{math}\frac{\partial{u_i}}{\partial{x_i}\partial{x_j}}{/math}
NOTE - replace the braces around math and /math with square brackets
will give you 
|
|
|
|

|
|
|
|
|
#7 |
|
New Member
Lee
Join Date: Nov 2020
Location: Taoyuan
Posts: 3
Rep Power: 6  |
Dear Gerry,
You are right! That is exactly my question. You did answer it. And I am glad to learn from you that most naturally occurring phenomena the differential order can be regarded as interchangeable. The problem of me is I need to know exactly the physics meaning behind the math. Otherwise, I can't really remember it. This is a very nice forum to know you and other people. And I finally know I need to learn Latex without second choice. I will keep studying what you and FMDenaro told me about tensor notation. I slightly touched the 4th order tensor when I studied the viscous shear stresses in a finite volume. Thank you Gerry! All the best, TommyWind |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
What I see, is a topic of the differential calculus, the mix derivative do commute under the
https://en.wikipedia.org/wiki/Symmet...nd_derivatives This is a classical topic and has nothing to do with the physics of the NSE. Just consider the regularity hypotheses. |
|
|
|

|
|
 |
| Tags |
| fubini, laplacian, navier stokes equation, viscous stress |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Implementing boundary condition as additional term in differential equations | MdoNascimento | OpenFOAM Programming & Development | 1 | March 25, 2015 12:48 |
| ATTENTION! Reliability problems in CFX 5.7 | Joseph | CFX | 14 | April 20, 2010 16:45 |
| Viscous term approximations | cfd_newbie | Main CFD Forum | 0 | November 28, 2005 21:23 |
| Re: viscous source term | mt | Phoenics | 10 | February 11, 2005 11:46 |
| Expression of 2ndary differential equation term | J.W.Ryu | FLUENT | 0 | June 18, 2002 00:50 |