 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
J.B.
Join Date: Jun 2020
Posts: 11
Rep Power: 6  |
Hi, I recently started using Einstein notation a lot from this paper [AGARD-R-819] for Favre averaging. However, I was never formally introduced to it academically. I was wondering if someone here could help me validate my confusion. I have 3 questions.
1. 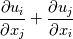 From the equation, what impact does it have if you switch the i & j. From my understanding, the answer is a scalar anyways so the order of the sum should not matter. I'm I correct? 2.The Kronecker delta basically tells us to sum the trace of a tensor. 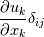 So here the k subscript is going to be k = 1, 2, 3. But why can't we write j instead? 3.Similarly from 2, 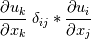 Is it still going to be the sum of the trace for both derivative term? Thanks for any input you can provide. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Chris DeGroot
Join Date: Nov 2011
Location: Canada
Posts: 414
Rep Power: 18  |
1. You are correct; you can switch the indices since they are arbitrary when both are being summed.
2. You can't write "j" in the derivative term and in the delta term because then you would have 3 j's, which is not allowed. If the index is repeated twice in implies a sum; if it appears once it is a free index. Having it 3 times would not make sense. You could switch the k to j, but then you'd have to make the j another letter (e.g. k). 3. The first term, for 3-space would be (du/dx + dv/dy + dw/dz). The second part, including the delta and the second derivative would be the same since it is only non-zero when i=j. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
|
I would add that:
1) You can switch indices when the quantity is symmetric with respect to those indices, a scalar being just a special case. Indeed, example 1 does not actually imply any summation (which is instead implied when the terms using the given index multiply each other), but it is a symmetric tensor ( 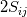 ). Also, the final result being a scalar doesn't automatically imply switchability of indices. For example, if you have a Levi-Civita symbol in your scalar expression (https://en.wikipedia.org/wiki/Levi-Civita_symbol), that scalar might change sign if switching indices improperly (a classical example being the triple scalar product). ). Also, the final result being a scalar doesn't automatically imply switchability of indices. For example, if you have a Levi-Civita symbol in your scalar expression (https://en.wikipedia.org/wiki/Levi-Civita_symbol), that scalar might change sign if switching indices improperly (a classical example being the triple scalar product).2) This is one of those cases where the official terminology really helps understanding what happens. More specifically, when an index has implied summation, like k in example 2, it is said to be saturated and you can't use it anymore. This is not much different from what happens when you integrate in a variable, by convention you don't reuse that variable in order to avoid confusion. In practice, for a saturated index you are actually free to use whatever you like, as long as that is not already used (so y, a, b, are all good replacements for k... j and i aren't). |
|
|
|

|
|
|
|
|
#4 |
|
New Member
J.B.
Join Date: Jun 2020
Posts: 11
Rep Power: 6  |
Thank you cdegroot and sbaffini for the valuable input. I will go on with my learning with what both of you suggested.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Confused by the tensor notation here | Astrokiwi | Main CFD Forum | 3 | May 27, 2015 13:14 |
| Simple vector notation help. uiuj in non index notation | meangreen | Main CFD Forum | 7 | October 7, 2012 12:07 |
| Help with einstein notation for a turbulence model | tstorm | Main CFD Forum | 4 | April 30, 2009 12:09 |
| Notation Standards and Uniformity | yNot | CFD-Wiki | 0 | April 5, 2008 16:00 |
| Question about tensor notation ! | Hyun | Main CFD Forum | 1 | November 19, 2004 07:29 |