 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Dustin Weaver
Join Date: Dec 2016
Posts: 4
Rep Power: 9  |
Does anyone know a detailed derivation of the k-omega SST turbulence model? I can't seem to find a fully derivation anywhere and yet a lot of people use this model quite frequently. I am having issues with going from the k-epsilon to the "transformed" k-epsilon in terms of omega.
The kinetic energy equation transformed derivation is straight forward but I'm struggling with dissipation. With the dissipation in the standard k-epsilon equation given by: ![{{D\varepsilon } \over {Dt}} = {C_{\varepsilon 1}}{\varepsilon \over k}{\tau _{ij}}{{\partial {u_i}} \over {\partial {x_j}}} - {C_{\varepsilon 2}}{{{\varepsilon ^2}} \over k} + {\partial \over {\partial {x_j}}}\left[ {\left( {\nu + {{{\nu _t}} \over {{\sigma _\varepsilon }}}} \right){{\partial \varepsilon } \over {\partial {x_j}}}} \right] {{D\varepsilon } \over {Dt}} = {C_{\varepsilon 1}}{\varepsilon \over k}{\tau _{ij}}{{\partial {u_i}} \over {\partial {x_j}}} - {C_{\varepsilon 2}}{{{\varepsilon ^2}} \over k} + {\partial \over {\partial {x_j}}}\left[ {\left( {\nu + {{{\nu _t}} \over {{\sigma _\varepsilon }}}} \right){{\partial \varepsilon } \over {\partial {x_j}}}} \right]](/Forums/vbLatex/img/186d9f4ce13c2b639dd3950424429951-1.gif) (eq1) (eq1)and using the ratio given by: 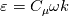 (eq2) (eq2)We now obtain 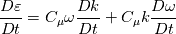 (eq3) (eq3)Plugging eq2 and eq3 into eq1 while putting a placeholder for epsilon constants with phi we obtain ![{C_\mu }\omega {{Dk} \over {Dt}} + {C_\mu }k{{D\omega } \over {Dt}} = {C_{\phi 1}}{C_\mu }\omega {\tau _{ij}}{{\partial {u_i}} \over {\partial {x_j}}} - {C_{\phi 2}}{C_\mu }^2{\omega ^2}k + {\partial \over {\partial {x_j}}}\left[ {\left( {\nu + {{{\nu _t}} \over {{\sigma _\varepsilon }}}} \right){{\partial \left( {{C_\mu }\omega k} \right)} \over {\partial {x_j}}}} \right] {C_\mu }\omega {{Dk} \over {Dt}} + {C_\mu }k{{D\omega } \over {Dt}} = {C_{\phi 1}}{C_\mu }\omega {\tau _{ij}}{{\partial {u_i}} \over {\partial {x_j}}} - {C_{\phi 2}}{C_\mu }^2{\omega ^2}k + {\partial \over {\partial {x_j}}}\left[ {\left( {\nu + {{{\nu _t}} \over {{\sigma _\varepsilon }}}} \right){{\partial \left( {{C_\mu }\omega k} \right)} \over {\partial {x_j}}}} \right]](/Forums/vbLatex/img/3ba16fce5c2de75b444faa289da3b177-1.gif) (eq4) (eq4)Some reducing and rearranging... ![{{D\omega } \over {Dt}} = {C_{\phi 1}}{\omega \over k}{\tau _{ij}}{{\partial {u_i}} \over {\partial {x_j}}} - {C_{\phi 2}}{C_\mu }{\omega ^2} + {1 \over {{C_\mu }k}}{\partial \over {\partial {x_j}}}\left[ {\left( {\nu + {{{\nu _t}} \over {{\sigma _\phi }}}} \right){{\partial \left( {{C_\mu }\omega k} \right)} \over {\partial {x_j}}}} \right] - {\omega \over k}{{Dk} \over {Dt}} {{D\omega } \over {Dt}} = {C_{\phi 1}}{\omega \over k}{\tau _{ij}}{{\partial {u_i}} \over {\partial {x_j}}} - {C_{\phi 2}}{C_\mu }{\omega ^2} + {1 \over {{C_\mu }k}}{\partial \over {\partial {x_j}}}\left[ {\left( {\nu + {{{\nu _t}} \over {{\sigma _\phi }}}} \right){{\partial \left( {{C_\mu }\omega k} \right)} \over {\partial {x_j}}}} \right] - {\omega \over k}{{Dk} \over {Dt}}](/Forums/vbLatex/img/f4c49cbd28eb56984dc0f1437fc56b5e-1.gif) (eq5) (eq5)I'm now stuck here and I believe just the last two terms are incomplete. My calculus is pretty rusty and not sure quite where to go. The transformed k-epsilon model stated by Menter,1994 is given by ![{{D\omega } \over {Dt}} = {{{\gamma _2}} \over {{\nu _t}}}{\tau _{ij}}{{\partial {u_i}} \over {\partial {x_j}}} - {\beta _2}{\omega ^2} + {\partial \over {\partial {x_j}}}\left[ {\left( {\nu + {\sigma _{\omega 2}}{\nu _t}} \right){{\partial \omega } \over {\partial {x_j}}}} \right] + 2{\sigma _{\omega 2}}{1 \over \omega }{{\partial k} \over {\partial {x_j}}}{{\partial \omega } \over {\partial {x_j}}} {{D\omega } \over {Dt}} = {{{\gamma _2}} \over {{\nu _t}}}{\tau _{ij}}{{\partial {u_i}} \over {\partial {x_j}}} - {\beta _2}{\omega ^2} + {\partial \over {\partial {x_j}}}\left[ {\left( {\nu + {\sigma _{\omega 2}}{\nu _t}} \right){{\partial \omega } \over {\partial {x_j}}}} \right] + 2{\sigma _{\omega 2}}{1 \over \omega }{{\partial k} \over {\partial {x_j}}}{{\partial \omega } \over {\partial {x_j}}}](/Forums/vbLatex/img/2cd925c4e0a312ca472445bc9b1a148e-1.gif) I've seen a lot of people just say that merely the addition of the last cross-diffusion term makes it an exact copy of the k-epsilon equation (that's what menter,1994 states as well) but I haven't seen a full derivation of this anywhere and so I'm not sure how that's the case. This being said, I feel I'm getting closer but my calculus is rusty and so any help will be greatly appreciated  . .
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
|
I suggest to give a look here
http://www.tfd.chalmers.se/~lada/pos...port_lowre.pdf and to the original references |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Dustin Weaver
Join Date: Dec 2016
Posts: 4
Rep Power: 9  |
This is a good reference and I'll go through this and post a reply. I already checked the original references and many others and they just say that the exact transformed k-epsilon equation merely has the addition of the cross-diffusion term. It seems that there is also a turbulent diffusion term that gets dropped out. I'm really surprised that I haven't found a full derivation when so many people use this model.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Turbulence Model switch RKE to K-omega SST | Astan | OpenFOAM Running, Solving & CFD | 3 | April 6, 2019 04:54 |
| Only two turbulence options available in CFX Pre | Jack001 | CFX | 5 | March 30, 2016 03:47 |
| Flow over a blunt body - SST turbulence model | bharath | CFX | 5 | January 29, 2016 11:16 |
| Overflow Error in Multiphase Modelling with Two Continuous Fluids | ashtonJ | CFX | 6 | August 11, 2014 15:32 |
| k omega turbulence model | sailspace | OpenFOAM Running, Solving & CFD | 0 | November 12, 2013 06:43 |