 |
|
|
[Sponsors] | |||||
Turbulence modelling using Machine Learning for Turbulent Channel Flow |
 4Likes
4Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
J.B.
Join Date: Jun 2020
Posts: 11
Rep Power: 6  |
Hi people! This is my first post here and hopefully it is at the right place. I am doing a master degree with focus on machine learning and turbulence modelling. After reading a few papers, one strategy consists of developing closures for the Reynolds Stress tensor using an infinite tensor polynomial (Pope 1975). The author mentions it's the most general expression. I know it is based on Cayley-Hamilton theory. However, I'm not really great at math and I would like to know if someone understands how the infinite polynomial was reduced to be the sum of 10 tensors, and what does invariants mean in this case? Looked into his manual but couldn't find the clarification that I need. Thanks
 https://www.reddit.com/r/CFD/comment..._learning_for/ |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
|
Can't really help now, but the fact that you posted it on reddit first and then came here, for some reason, reminds me of the prodigal son parable
 But, let's first start from a simple fact: do you understand the basis of Cayley-Hamilton theorem (https://en.wikipedia.org/wiki/Cayley...milton_theorem)? In that case one would only need to explain why exactly 10 tensors Second: very roughly, an invariant of a tensor is some quantity that, if tensor is transformed into another reference frame, still has the same value (but someone more into math might certainly give you a better deinition... including wikipedia, I guess https://en.wikipedia.org/wiki/Invariants_of_tensors) For reference, the original work mentioned by op is here https://tcg.mae.cornell.edu/pubs/Pope_JFM_75.pdf Last edited by sbaffini; June 7, 2020 at 05:09. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,747
Rep Power: 66    |
It's explained in detail for the 2D case in the appendix. So are you able to follow that? If not, which parts are confusing?
For 3D, we just need to repeat the same stuff in the appendix to derive the 10 independent tensors. For this, a hint is that it's related to the n-th power of a matrix property which you can get from the Wiki article. There is a reference for the derivation in the 3D case. Nonetheless, the 10 independent tensors in 3D are given. Another hint is that we are looking only for tensors that are symmetric and have zero trace. |
|
|
|

|
|
|
|
|
#4 |
|
New Member
J.B.
Join Date: Jun 2020
Posts: 11
Rep Power: 6  |
Hi sbaffini, thanks for the reply! My understanding of the Cayley-Hamilton theorem is basic. I know that if a matrix is the argument of their own characteristic equation then it is a solution and equals 0. As for invariants, I also have roughly the same idea as you. I know from Pope that the invariants are scalars obtained from the tensors but could there be a physical meaning behind let's say {S^2} which is if I am correct S_ii^2?
|
|
|
|

|
|
|
|
|
#5 |
|
New Member
J.B.
Join Date: Jun 2020
Posts: 11
Rep Power: 6  |
||
|
|

|
|
|
|
|
#6 |
|
Senior Member
|
Cayley-Hamilton here means that a tensor fullfills its own characteristic polynomial equation, so in 3D you can express
 as function of as function of 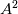 , ,  , ,  and the invariants of and the invariants of  . .It is then easy to see that, because 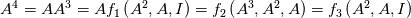 , you can also express higher powers of A with powers up to the second by repeatedly substituting , you can also express higher powers of A with powers up to the second by repeatedly substituting  . .All this machinery only serves the purpose to justify the fact that whatever power series of 3D second order tensors can be expressed as just a second order polynomial in the tensor, whose coefficients are functions of the tensor invariants. The invariants are the coefficients of the characteristic polynomial but, coming from the actual tensor and being invariant to frame rotation, they typically bring physical meaning. For example  , when applied to , when applied to 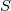 , is the divergence of the velocity field. Other familiar terms may or not come out, depending on the tensor you are working on and the field (note that Pope includes turbulence terms in his definition of s). , is the divergence of the velocity field. Other familiar terms may or not come out, depending on the tensor you are working on and the field (note that Pope includes turbulence terms in his definition of s).Now, what really complicates the matter here is the fact that you have a dependence from both S and W, but you also have that a, the quantity that it is looked for (the non-dimensional Reynolds stress) is symmetric and zero trace (because the flow is assumed incompressible). Personally, also because of the lengthy procedure in 3D, I always took for granted the last step: the independent invariants and tensors that you can build from S and W that are also symemtric and zero trace are those reported in the paper (section 3). To grasp the reasoning behind this in 2D, you have to go to the appendix (or look for the extended works of Spencer and Rivlin on the subject). Note that A4 doesn't come from the previous equations, it is just a starting hypothesis, that is you assume to have a polynomial whose general term woul look like P. I have difficulties in proving A3 without pencil and paper but, after that, everything should just follow easily. Last edited by sbaffini; June 10, 2020 at 04:40. |
|
|
|

|
|
|
|
|
#7 |
|
New Member
J.B.
Join Date: Jun 2020
Posts: 11
Rep Power: 6  |
Hi sbaffini, your input has clarified some confusion that I had. Thank you!
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| kOmegaSST without turbulence modelling of the flow around geometry | CFDnewbie147 | OpenFOAM Running, Solving & CFD | 7 | December 5, 2013 08:29 |
| Modeling the mixing of air and kerosene in a flow channel | StefanG | CFX | 3 | June 11, 2012 21:21 |
| About Turbulence Intensity (Pipe flow assimilated) | gRomK13 | Main CFD Forum | 1 | July 10, 2009 04:11 |
| Advice on multi-phase flow modelling | Martin | Main CFD Forum | 3 | October 14, 2008 06:16 |
| Code release: Flow Transition and Turbulence | Chaoqun Liu | Main CFD Forum | 0 | September 26, 2008 18:15 |