 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Art Mis
Join Date: Apr 2020
Posts: 6
Rep Power: 6  |
Hi there,
From Reference: http://www.ifh.uni-karlsruhe.de/lehr...pt/ed2/ch3.PDF I have some troubles to understand how we go from equation 3.9 to 3.11. I get that derivative and averaging are commutative but why the derivative with respect to the averaged concentration is not 0 ? Thanks a lot ! |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,865
Rep Power: 73    |
Quote:
The chapter confuses the concept of statistical time averaging (or ensemble averaging) in the Reynolds averaging formulation (RANS) and that of a finite time-averaging illustrated in the section. I suggest to disregard this text and have a look to the textbook of Wilcox. |
||
|
|

|
||
|
|
|
#3 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,750
Rep Power: 66    |
This happens only when you average for infinite time. Here they are doing a finite-time average and hence the time-average can still change in time. What is there is not incorrect per se, but it can be confusing for the reasons Filippo mentioned. It would be much clearer if they presented it as an ensemble average.
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,865
Rep Power: 73    |
The textbook of Wilcox is available here https://epdf.pub/queue/turbulence-mo...d-edition.html
I suggest a reading of Chap. 2 |
|
|
|

|
|
|
|
|
#5 | |
|
New Member
Art Mis
Join Date: Apr 2020
Posts: 6
Rep Power: 6  |
Thanks a lot for the book, I went into the Chapter 2 and it's not quite obvious why it is better to present the results as an ensemble average instead of time average, could you develop please ?
I get why they don't use a spatial averaging (because the flow is not homogeneous), but how do we know that we should use an ensemble average instead of spatial or time averages ? And what does it changes in the way the equations are solved ? Quote:
Does it mean that we have something like histograms where we have a "local average" during the time interval equal to the width of each column? I have some troubles to visualize the concentration evolution with time. Plus, how do we define this "finite-time" for the average, what are the conditions that have to be fulfilled ? Sorry for the naive question, I am very new to this and thanks a lot for your precious help ! |
||
|
|

|
||
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,865
Rep Power: 73    |
Quote:
Think about the original experiment of O. Reynolds, he did several realizations of the famous experiment. If you take the ensemble average of a number of realizations tending to +Inf the result is that you have a statistically steady field (no time derivative on the ensemble-averaged varaible). If the flow has the proper condition to ensure ergodicity, such result is the same if you use the statistical time-averaging (the period T tending to Inf) and the result is that the RANS equations are steady. Now, if you have a flow driven by an external force, for example by a piston moving periodically in a cylinder, the ensemble averaging (even for infinit number of realization) produces a statistical field that is no longer steady, at each time the field is the result of the ensemble averaging but is different from time to time. If the time averaging is local, that is f_bar(x,t) = 1/t Int[t0,t] f(x,t') dt' this is a function of time defined by an integral function. It can be considered like a filter in time (as happens in LES) and is no longer a statistical averaging. The result is that the equations are filtered in time but are not steady. Furthermore, the cross term do not vanish as happens in RANS. The key to understand is the physics of the flow problem, if it has a statistical steady energy equilibrium or not. |
||
|
|

|
||
|
|
|
#7 | |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,750
Rep Power: 66    |
Quote:
Eq. 3.7 in the text is a windowed average / temporal filter. But 3.8, 3.9, 3.10, 3.11 are actually results that you get from an ensemble average. With a windowed function, the windowed-average and time-derivative do not commute and you do not have 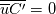 and and 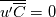 . Nor can you drop the double overbar, . Nor can you drop the double overbar, 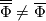 . Given that they used all the properties one would obtain with an ensemble average, I think they inserted 3.7 by mistake. But in either case, the time-derivative is non-zero (for both a local average and an ensemble average). The time-derivative is in general non-zero. It is zero if you average or take ensembles from t= -infinity to t=+infinity & for special cases. . Given that they used all the properties one would obtain with an ensemble average, I think they inserted 3.7 by mistake. But in either case, the time-derivative is non-zero (for both a local average and an ensemble average). The time-derivative is in general non-zero. It is zero if you average or take ensembles from t= -infinity to t=+infinity & for special cases.
|
||
|
|

|
||
|
|
|
#8 |
|
New Member
Art Mis
Join Date: Apr 2020
Posts: 6
Rep Power: 6  |
Quote:
Thanks a lot to both of you for these answers. To summarize: 1) If I develop the equations using time-averaging instead of ensemble averaging, I have to justify that the flow do not decay with time. I did not really understand though why with time averaging the operators (average/derivative) do commute but not with ensemble averaging ? Plus, how do you know that the equations you cited from the link I've sent come from ensemble averaging since they do not average on a number of experiments but only on time ? 2) In reality we're looking at the derivative of the average concentration on a finite-time period (how can we define the correct window period ?) and NOT the derivative of a an averaged concentration over a infinite period, which will end up being 0. Does the chosen finite-period have to be the same for concentration and velocity averages ? 3) Then, when dropping the overbars, it means that 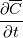 = = 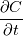 . . Does it means that the concentration 'function' is redefined is the sense that the new function is made by considering each finite time-averaged periods (instead of the initial concentrations values) ? Is it always true ? I'm not sure to get a deep understanding of this. Thank you very much. |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,750
Rep Power: 66    |
1) Either 3.7 is slightly wrong or the rest of the entire document is slightly wrong. If they had used the temporal filter, they would get equations that look like the ones in LES (equations with cross-terms and with double overbars). See properties of a filter. Three properties are called upon: commutativity, cross-terms going to zero, and able to drop overbars.
Since they used all the properties of a Reynolds operator and did not consider any of the cases where these properties don't hold (i.e. they did not provide justification for these properties to hold), this leads me to believe that they did indeed use a Reynolds operator and not a temporal filter such as that given in Eq. 3.7. Again, what is there is not wrong per se, but it's not right either. 2) There isn't an incorrect window. All windows are valid. It's a low-pass filter and you can choose the cutoff to be any frequency (timescale) that you like. But if you choose the window to be very very long relative to any flow timescale, then your temporal filter will not filter anything and your windowed average and statistical average will be practically the same. Still, it does not change that with one method you should obtain a certain set of equations and a different set of equations with another averaging method. 3) After you apply the eddy viscosity hypothesis (Eq. 3.12) you will arrive at Eq. 3.14 (but with overbars) which turns out to be the same as the time-accurate governing equation that you started with (except that you have an effective diffusion coefficient). Dropping the overbars is just lazyness. There should be overbars. They changed their notation on-the-fly is what happened. |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,865
Rep Power: 73    |
Quote:
Be aware that the ensemble averaging makes sense either for statistically steady or unsteady turbulence. If the ergodicity property applies then the ensemble averaging and the infinite-period time averaging tends to the same result. Considering the finite-time averaging (a local filtering in time) the time derivative and the time averaging do commute exactly if the window is constant in time. Again, I strongly suggest to follow a good textbook not those notes |
|
|
|

|
|
|
|
|
#11 |
|
New Member
Art Mis
Join Date: Apr 2020
Posts: 6
Rep Power: 6  |
Hi there,
Again thanks a lot and sorry for my late answer, I was busy elsewhere. I'll explain what I've understood so far (please correct me if I'm wrong) with few additional questions related to one misunderstanding regarding the differences between time-averaging and finite-time averaging. Due to the used properties (double average = simple average, cross-terms non-zero), time-averaging has been used and the properties of the Reynolds operator are at play. However, you both said that eq. 3.7 of the link I've posted (why only this one? because in the following eq. the properties of the Reynold operator are used?), corresponds to a local-filtering (LES rules) because the integral is applied over a finite-time period. However in the textbook of Wilcox, time averaging is also presented using t -> t+T (with T being finite). Plus, if I quote Wilcox ''the time average of an unsteady term like du/dt is obviously zero for stationary turbulence'' (between eq. 2.11 and 2.12), which confuses me a bit. What confuses me is : I understood that 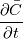  0 because the average period is finite (T) and hence the concentration or velocity averages can still vary in time. But why a time-average is presented over a finite-time period (to me it should be infinite) and hence what are the differences with a temporal filter/finite time averaging ? 0 because the average period is finite (T) and hence the concentration or velocity averages can still vary in time. But why a time-average is presented over a finite-time period (to me it should be infinite) and hence what are the differences with a temporal filter/finite time averaging ?Again thank you so much, the subject becomes much clearer thanks to you ! |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Determination of the time period for averaging of the velocity field at periodic flow | mo92 | OpenFOAM Running, Solving & CFD | 0 | December 18, 2018 13:24 |
| Difference of averaging and filtering in RANS and LES | Friendly | Main CFD Forum | 1 | February 1, 2018 18:43 |
| LES Time averaging Huge Oscillations | Mirage | OpenFOAM Programming & Development | 1 | January 27, 2017 11:20 |
| Starting field averaging using libFunctionObject after certain time | eelcovv | OpenFOAM Programming & Development | 25 | December 7, 2015 23:28 |
| When to use mass flow averaging | cspectre | CFX | 2 | December 6, 2009 06:30 |