 |
|
|
[Sponsors] | |||||
Rationale for having filter for turbulence flow |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Join Date: Feb 2019
Posts: 69
Rep Power: 7  |
"In LES, a low-pass filtering operation is performed so that the resulting filtered velocity field U can be adequately resolved on a relatively coarse grid."
From the above statement, can I interpret that the reason for having a low pass filter especially in turbulent flow is to eliminate oscillations when coarse grid is used? These oscillations are actually eddies smaller than the grid spacing but because coarse grids are used, they come off as oscillations. Thus, am I right to say that the low pass filter used for LES is to have a non-oscillatory flow that can still generate eddies (size larger than grid spacing) for coarser grids? |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
The idea is that the action of the filter makes "smooth" the variable and, consequently, be better representable on a grid of reasonable size. That makes sense only for turbulent flows. The term "non-oscillatory" is not correct, the filtered field has a wide range of resolve components producing an unsteady field with eddies from the integral to the cut-off lenght scale. |
||
|
|

|
||
|
|
|
#3 |
|
Member
Join Date: Feb 2019
Posts: 69
Rep Power: 7  |
Thanks for the response. However, I do not have enough cfd experience to understand the significance of representing the effect of unaccounted eddies with turbulence models. Why can't DNS (I assumed is just the full Navier Stokes equation) just be used on a coarser grid? I imagine eddies with lengthscale smaller than grid size will not be capture by the solver and thus, won't this eliminate the small eddies naturally?
Unless we need LES for problems where the turbulent flow started initially from small eddies which need to be resolved? For instance, the Kelvin-Helmholtz instability will not occur if the grids are not fine enough... |
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
From a theoretical point of view, owing to the non-linear coupling, the components of the flow that are cutted away by the filtering still affect the resolved filtered components. That justifies the need of an SGS model |
||
|
|

|
||
|
|
|
#5 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,754
Rep Power: 66    |
Just to clarify a little bit more. I would add that non-linear behavior is also the reason we need turbulence models in RANS. In RANS, you apply a temporal filter instead of a spatial one. You still need to account for the influence of the cutted away stuff. You don't need to explicitly know all the details of the things being cutoff, just their influence. The slightly more detailed explanation is:
Statistically, if I have two random variables  and and 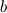 and let <> brackets denote my linear filtering operator. I can decompose my variable into two parts, and let <> brackets denote my linear filtering operator. I can decompose my variable into two parts,  and and  , the first which survives the filtering operator and the second which is eliminated by it. That is, I define: , the first which survives the filtering operator and the second which is eliminated by it. That is, I define: under that condition that under that condition that and and  Under operations like addition we are still linear:  Looks pretty promising... Until you try to filter other things like products of variables.  which turns out to be: which turns out to be:  or equivalently or equivalently 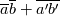 That last thing is the stuff that is not cutoff by our filtering operation... Yikes! Well, we don't need to entire details of  and and  , that would require that we know , that would require that we know  and and 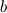 . We only ask that we know the influence of . We only ask that we know the influence of 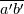 in causing in causing 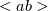 to deviate from to deviate from  And that's why you need a SGS model in LES and a "turbulence model" in RANS. But in both cases, you are not modeling  and and  , you are modeling only their influence , you are modeling only their influence 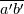 And that's why coarse-grid DNS is not DNS but actually a no-SGS LES. In a coarse-grid DNS, you are effectively pretending that  which you know is incorrect because which you know is incorrect because 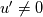 whenever something has been cutted off (the smaller eddies). True DNS, nothing is being cutted off by the filter and you recover whenever something has been cutted off (the smaller eddies). True DNS, nothing is being cutted off by the filter and you recover 
|
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
Correct, just a note on the LES decomposition where, differently from RANS, the mixed term (a' b_filt)_filt does not vanish |
|
|
|

|
|
 |
| Tags |
| conceptual, turbulence |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Nanofiber filter flow analysis | Balasankar | FLUENT | 0 | September 18, 2016 12:45 |
| Dynamic Smagorinsky model- Filtering Concept | saeedi | Main CFD Forum | 34 | November 29, 2015 23:43 |
| simulate reverse flow for filter cleaning | Rashmi | FLUENT | 2 | January 13, 2007 07:38 |
| computation about flow around a yawed cone | Tylor Xie | Main CFD Forum | 0 | June 9, 1999 08:33 |
| Flow through a screen filter | Ismail Guler | Main CFD Forum | 1 | September 11, 1998 03:13 |