 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Numan Mazumder
Join Date: Jan 2019
Location: India
Posts: 35
Rep Power: 7  |
I am trying to solve the Navier Stokes Equation (2D) for Spherical Co-ordinates using FVM. I have come across a source term in derivative form.
My souce term is 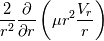 Now after integrating the above term along with north&south faces of the control volume, we can write it as-- ![2\left[ \left(\mu r^2 \frac{V_r}{r} \right)_n - \left(\mu r^2 \frac{V_r}{r} \right)_s\right]\triangle\theta sin\theta_p 2\left[ \left(\mu r^2 \frac{V_r}{r} \right)_n - \left(\mu r^2 \frac{V_r}{r} \right)_s\right]\triangle\theta sin\theta_p](/Forums/vbLatex/img/a391f06218148cede7ea31d6942a0cca-1.gif) which can be further simplified as ![2\left[\mu_{n}\left(area\right)_n\left(\frac{V_r}{r}\right)_{n}-
\mu_{s}\left(area\right)_s\left(\frac{V_r}{r}\right)_{s}\right] 2\left[\mu_{n}\left(area\right)_n\left(\frac{V_r}{r}\right)_{n}-
\mu_{s}\left(area\right)_s\left(\frac{V_r}{r}\right)_{s}\right]](/Forums/vbLatex/img/c0ff2bb0d6e22612cd6dde31f3377af8-1.gif) where 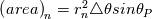 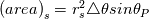 My questions are. 1. Should I interpolate the velocity to the main grid point from north and south faces? 2. After interpolating, should I used the old values for the source term? 3. Is there any other way to handle this kind of source term? 4. For source term linearization, as per Patankar formulation S=Sc+Sp.U Can I have source terms in other grid points also? I mean to say, as like S= Sc+Sp.U Can I have S=Sc+Sw.U, S=Sc+Sn.U, S=Sc+Ss.U, S=Sc+Se.U ? 5. Can you please suggest me any good book/reference for my query? Regards. Numan Siddique siddiquesil@gmail.com |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
What is wrong with your approach is that you are writing the equations for a finite difference scheme...conversely, you must start from the general conservative form and write the integral of the fluxes. Have a look for example to this paper https://arxiv.org/abs/1404.0537 |
||
|
|

|
||
|
|
|
#3 |
|
Member
Numan Mazumder
Join Date: Jan 2019
Location: India
Posts: 35
Rep Power: 7  |
Thank you for your reply.
I have discretized the N.S equation for spherical coordinate using Finite volume method. Here are the full details of the discretization scheme where I have used the flux term. Navier Equation for spherical coordinate in r-direction is given as 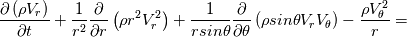 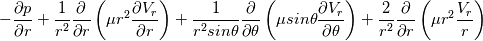 After rearranging the convection-diffusion term, the above equation can be written as 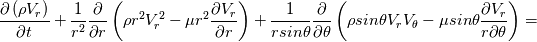 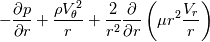 which can be written by using flux term  where the fluxes are defined as 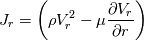 , , 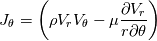 In the above equation, all the term of the right-hand side is source terms. First two-term of the right-hand of the above equation can be easily found out. Pressure term is hand via the SIMPLER algorithm. My doubt is about the 3rd source term of the right-hand side of the equation. |
|
|
|

|
|
|
|
|
#4 |
|
Member
Numan Mazumder
Join Date: Jan 2019
Location: India
Posts: 35
Rep Power: 7  |
after discretization of the above equation, the final form can be written as.
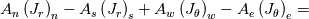 ![A_e(P_E-P_W)+\left(\frac{\rho V_\theta^2}{r}\right)_P \triangle V+2\left[A_n\left(\frac{V_r}{r}\right)_n-A_s\left(\frac{V_r}{r}\right)_s\right] A_e(P_E-P_W)+\left(\frac{\rho V_\theta^2}{r}\right)_P \triangle V+2\left[A_n\left(\frac{V_r}{r}\right)_n-A_s\left(\frac{V_r}{r}\right)_s\right]](/Forums/vbLatex/img/3c9583b271a8ceecf05b1c860632924f-1.gif) Where, 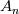 = area of the north face = area of the north face = area of the south face = area of the south face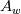 =area of the west face =area of the west face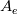 =area of the east face =area of the east face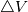 = volume. = volume.My questions are only about the last term. 1. How to handle the last term of the above equation? 2. Should I interpolate the value of north&south faces to the main grid point for the last term? 3. Can I write the last term as S=Sc+Sn.V & S=Sc+Ss.V as like S=Sc+Sp.V? |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Actually, there is no source term in the momentum equation. A source term is something that must be added explicitly as a consequence of a physical external forcing.
From what you wrote I see you are not focusing the fact that in a FVM the fluxes must be written to ensure conservation. You haven't read the paper I linked. |
|
|
|

|
|
|
|
|
#6 |
|
Member
Numan Mazumder
Join Date: Jan 2019
Location: India
Posts: 35
Rep Power: 7  |
Thank you very much. Finally, I have understood my mistakes as there would not any extra terms as a source in the momentum equation apart from the pressure, and centrifugal forces in my case. I would like to read the reference provided by you. Thank you again.
 regards: Numan Siddique Mazumder. India |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [Other] Tabulated thermophysicalProperties library | chriss85 | OpenFOAM Community Contributions | 62 | October 2, 2022 04:50 |
| [swak4Foam] swak4foam for OpenFOAM 4.0 | mnikku | OpenFOAM Community Contributions | 80 | May 17, 2022 09:06 |
| [swak4Foam] funkyDoCalc with OF2.3 massflow | NiFl | OpenFOAM Community Contributions | 14 | November 25, 2020 04:30 |
| Trouble compiling utilities using source-built OpenFOAM | Artur | OpenFOAM Programming & Development | 14 | October 29, 2013 11:59 |
| [swak4Foam] Error bulding swak4Foam | sfigato | OpenFOAM Community Contributions | 18 | August 22, 2013 13:41 |