 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 15  |
I believe the following requirements should be satisfied by the discretization to be conservative is prescribed by different researchers. If I'm missing some points please inform me. I have also included my personnel opinion on the requirements:
1) It should have a unique flux at a point (cell face). Reason: Most of the cases, especially steady-state, the spatial fluxes are the conserved (eg) Fourier law of conduction. 2) The governing equation should be in conservative form Reason: Typically we need this requirement for solving a problem involving shocks or discontinuity. That is because in high speed flows shock speed is calculated based on Runge Hugoniot jump conditions. That is defined for a conservative form of governing equation. Unfortunately, I'm not aware of any shock speed calculation for non-conservative form. If we use the non-conservative form, it will lead to wrong shock speed. 3) The quantity sitting in the divergence term of governing equation should be physically conservative. If the quantity sitting in the derivative is not a physically conservative variable that cannot be a conservative discretization. Reason: Just by writing the governing equation in divergence form cannot make the discretization conservative. This is illustrated in the book "Riemann Solvers and Numerical Methods for Fluid Dynamics " in the third chapter, subsection "Conservative Versus Non–Conservative Formulations". 4) Typically these equations written in the conservative form are integral in nature. Reason: We do have finite cells in discretization so integral form make more sense than differential form. 5) The change of conservative variable overtime should be balanced only by the boundary terms. In other words, non-physical internal source or sink should not be in the discretization. 6) For steady-state, the inflow flux should equal to outflow flux of the boundaries (This is almost similar or consequence of point no 1). Reason: Since most of the computations carried at the development of FVM is for the steady-state equation so they want the spatial fluxes to be conserved. In case of a transient problem, I'm not sure about this requirement, because 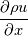 is not a conserved quantity, only is not a conserved quantity, only  is a conserved quantity. Though the non-conservative form and conservative form of GDE are mathematically equivalent, they are numerically not the same. Typically the error induced by non-conservative form is relatively more than conservative form. I hope this is marginal for incompressible flow because a large number of researchers from the incompressible community using the non-conservative form and prescribing it. I personally did not validate this. If anybody carried this, please share it. is a conserved quantity. Though the non-conservative form and conservative form of GDE are mathematically equivalent, they are numerically not the same. Typically the error induced by non-conservative form is relatively more than conservative form. I hope this is marginal for incompressible flow because a large number of researchers from the incompressible community using the non-conservative form and prescribing it. I personally did not validate this. If anybody carried this, please share it. Though these requirements are put forward in different kinds of literature, I believe, the real conservativeness can be achieved only when the solution exactly satisfy the governing equation. We cannot achieve such a solution using existing methods, because of a lot of errors introduced by the different steps by the algorithm. All equivalent differential equations of different schemes are not the same as the original governing equation. If the scheme cannot satisfy the original differential equation, I believe calling one scheme conservative scheme is quite odd for me. It may satisfy the governing equation when the grid size approaches to zero. I believe all the consistent numerical schemes satisfy that property and it is the essence of numerical methods. I believe the term "conservative discretization" or "conservative scheme" is just terminology. The schemes based on "conservative discretization" cannot really a conservative one or I would say all the consistent and stable numerical schemes are conservative. If the scheme is really a physically conservative, it should able to give good result. But after satisfying conservativeness, we expect the scheme should have other properties like monotonicity, positivity, entropy stability, energy positivity etc. Some papers are claiming that their schemes are satisfying those criteria but they are also giving oscillations even on some 1-D test cases with some complicated initial conditions. For me, the word "conservative discretization" is absurd or do we need to incorporate more requirements to be a scheme to be conservative now and in future, still we reach an ideal definition? Please don't fix yourself with existing literature, try to think general based on our fundamental understanding. I like to get your opinion on this, thank you. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
"If the scheme cannot satisfy the original differential equation, I believe calling one scheme conservative scheme is quite odd for me. "
No, that is not exactly true... I agree that the numerical discretiation produces a solution that does not satisfy the original PDE but it satisfies the modified PDE. If you look at the modified PDE for conservative and non conservative discretizations I will get the issue: the modified PDE for the conservative discretization is still in conservative form, it just modified the flux in the original PDE. Have a look here https://www.researchgate.net/publica...mes_simulation |
|
|
|

|
|
 |
| Tags |
| conservative form, finite volume method, non conservative form |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Unknown function type pressureTools | Dorian1504 | OpenFOAM Post-Processing | 23 | May 25, 2021 10:24 |
| problem during mpi in server: expected Scalar, found on line 0 the word 'nan' | muth | OpenFOAM Running, Solving & CFD | 3 | August 27, 2018 05:18 |
| [OpenFOAM] Take derivative of mean velocity in paraFoam | hiuluom | ParaView | 13 | April 26, 2016 07:44 |
| [OpenFOAM] Annoying issue of automatic "Rescale to Data Range " with paraFoam/paraview 3.12 | keepfit | ParaView | 60 | September 18, 2013 04:23 |
| error while compiling the USER Sub routine | CFD user | CFX | 3 | November 25, 2002 16:16 |