 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 14  |
What is conservative discretization and what are the requirements it should satisfy to be a conservative discretization? Why FVM is conservative scheme?
The integration of governing differential equation (GDE) over the cell and discretizing the equation that we call as conservative discretization 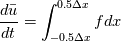 Is there is any rule that the limit should be from -0.5 to 0.5? why not -0.3 to 0.7? or 0 to 1? will it cause an error because of not having symmetricity? How can one say this equation is conservative but FDM (differential form) is not conservative? but both of them satisfy the governing equation. Why any scheme that satisfies the governing equation cannot be a conservative method? Assuming that the equation in conservative form (mathematically conservative form). Thank you. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
Your question is basically a homework of a CFD student, you can find the answer in many CFD textbooks. Start to write the integral form of the equations, you will see that FVM are deduced from this continous formulation that is conservative by definition |
|
|
|

|
|
|
|
|
#3 | |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 14  |
Quote:
Why do all the FVM formulations use -0.5 to 0.5? Is there is any physical significance? Thank you. |
||
|
|

|
||
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
This principle is intrinsic in the Reynolds transport theorem and has nothing to do with a nunerical topic. It is a physical fundamental principle that we simply want to fulfill numerically. The question about \-0.5 in the integral is not well posed. You must write the volume integral over a certain finite volume. In the integral must appear the widths of the volume. |
||
|
|

|
||
|
|
|
#5 | |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 14  |
Quote:
I like this answer because the standard "telescoping property" definition does not involve time variation, I think you have included that in this definition. Can I consider this answer as "telescoping property" that considered time variation effects? All the conservative discretizations I read in books and paper are in the intergral form. I like to know your opinion on: can only the integral form can make the scheme conservative but not the differential form provided that the GDE is in the conservative form? Thank you. |
||
|
|

|
||
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
Definitely yes, the telescopic property is included in my definition. Fro steady flow it implies that the summ of all the fluxes must vanishes but in the unsteady case (as originally formulated by the Reynolds theorem), the summ of all the fluxes results in the time variation of the volume averaged variable (note how is a function only of the time for a fixed volume). The discrete conservation property can be "extended" somehow also to the differential divergence form where the time derivative of the pointwise variable depends only on the divergence of the fluxes. Once computed a flux it must be unique for two adjacent cell. What is theoreticall questionable is the denomination of conservation for a pointiwise variable. It has no sense to define a conservation property of a quantity when you measure it on a volume of vanishing measure, that is on a mathematical point. For this reason I always consider the integral form as the natural one for the FV discretization. |
||
|
|

|
||
|
|
|
#7 | |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 14  |
Quote:
|
||
|
|

|
||
|
|
|
#8 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
But you do not need to invoke the convergence of the FV-based solution towards the differential one... In other words, you can compute the weak solution without the need to invoke the continuity of the function. Be aware that you can find in literature the differential equation but that implied the commutation of the averaging and differential operators so that the PDE acts on the locally averaged variable not on the pointiwise variable. This is the basis on the hystorical LES approach that use the volume averaging as filter. |
||
|
|

|
||
 |
| Tags |
| conservative form, finite difference method, finite volume method |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Radiation in semi-transparent media with surface-to-surface model? | mpeppels | CFX | 11 | August 22, 2019 08:30 |
| My radial inflow turbine | Abo Anas | CFX | 27 | May 11, 2018 02:44 |
| conservative or non conservative, Is there a big difference? | sharonyue | OpenFOAM Running, Solving & CFD | 1 | April 10, 2015 05:19 |
| Question about heat transfer coefficient setting for CFX | Anna Tian | CFX | 1 | June 16, 2013 07:28 |
| Replace periodic by inlet-outlet pair | lego | CFX | 3 | November 5, 2002 21:09 |