 |
|
|
[Sponsors] | |||||
Convection - Diffusion Spectral Study for Finite Difference Methods |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
|
Dear community, I read a very good paper that it is definitely worth reading. I definitely encourage the reading:" Spectral analysis of finite difference schemes for convection diffusion equation". Suman et all. Computer and Fluids 150(2017)95-114. https://www.researchgate.net/publica...usion_equation
The authors presented a great analysis in the spectral domain of different temporal-spatial discretization techniques which results are extremely interesting. However, I have a couple of questions that I'd like to know your opinion and suggestions. 1.- The authors used a lot of complex properties and operation. I think that people that work with spectral methods understand this easily. Is there any resource you could suggest. For example, the derivation of the equations shown in Part 2 was difficult to really understand. 2.- Equation (9) represents the physical amplificationf factor, taht for this specfici case (convection- diffusion) has an analytical representation. 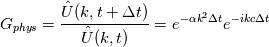 However, the text says that the absolute of G is the amplification factor. What I understand is the following. If the value of equation (9) is greater than 1 then the system is not damped at all and it will evolve to an unstable state, therefore diverging. Similarly for negative values. Therefore, a monotonical solution will require to G be between 0<G<1. Am I right? Each numerical implementation (scheme) has its own amplification factor and the authors exploited this fact, and therefore they obtained the ratio between the [math]G_{phys}/G_{num}[math]. However, the [math]G_{num}[math], required the derivation of its analytical counterpart. I guess that is not straight forward for all schemes, for example, FVM. Or what if I have cell center or vertex center methods, or even an averaged method. How can I get the analytical counterpart? Is it possible to get the FFT of the solution at two subsequent time steps and obtain the ration in this way? However, I think that in the initial transient part where the solution hasn't evolved to the attractor the ration could be completely wrong since it is just a numerical transient phenomenon. 3.- An striking fact, is that for Euler - central difference for the convective and diffusive term, the instability region is shown in Figure 2 is considers areas with CFL way lower than 1....Jum interesting. For the same scheme but larger Peclent number, the stable region is completely different, with the lowest CFL being exactly 1 for all wavenumbers. This lead to the next question, does the instability born and grow in a specific wavenumber? Refer to figures 2-9 from paper. Finally, the authors referred to diffusion when my conclusion is that G is more related to the dissipation. Diffusion is driven by gradients whereas dissipation is more a numerical issue because of truncation terms. For example closing paragraph from section 3.3. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Hello Julio
I read that paper some time ago, Part 2 is based on the transformation of the original PDE in the Fourier space. Then the resulting ODE is integrate and provides the Gphys expression. This amplification factor is exact and describes the exact solution of the PDE therefore it cannot be used for studying the numerical instability. For that you should see the Gnum factors. As you wrote, each numerical scheme produces its Gnum factor. It does not change in time therefore has nothing to do with the initial numerical transient. Numerical stability is analysed for any initial solution. I am not sure to understand your question #3 |
|
|
|

|
|
|
|
|
#3 | ||
|
Senior Member
|
Thank you very much professor for your valuable time. Your inputs is always apprecaited!
Quote:
Quote:
Professor I have uploaded two pictures. One is called 1 and the other one is called 3. The file named 1 represents the Euler - central scheme for the convective and diffusive term. The second file (2) represents the same discretization technique but the Peclet number is 0.5, whereas the first picture represent a case with Peclet number of 0.01. I am surprised that the unstable region is completely different. For the picture one it clearly shows that wavenumber largers than 3 are stable for all CFL numbers. 1.jpg 3.jpg The follwing picture (2) represents the solution of Runge Kutta with compact scheme. 2.jpg My question is more about the source of the instability. After looking at this picture I wonder if the culprit is one specific wavenumber. For example, picutre 2 shows that the wavenumber 2 is stable for CFL = 1.2, but the same wavenumber falls into the unstable region for CFL larger than 1.4. That is why I ask about the growth and source of instability. Finally, the author uses diffusion where my conclusion is that G represents the dissaption and not diffusion, am I right ? |
|||
|
|

|
|||
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
The amplification factor Gnum is obtained from the numerical scheme when you insert the generic Fourier component Fk(t)*exp(i*k*x) in each term. This is the numerical solution you are supposing. When you analyse the numerical stability analysis we do not invoke a specific transient, the absolute stability requires that the solution is bounded for any initial condition and, therefore, for any numerical transient.
The relevance of the initial conditions can be to rapidly excite the highest resolved wavenumbers if are already present in the initial prescription. When you consider a convection-diffusion equation the best way to analyse the stability issue is to consider the plane Cfl-Peh. That is a map in which you see the curve Cfl(Peh) representing the limit of the stability reagion. This map is obtained in doing the evaluation of the amplification factor in the most critical situation (in the sense for all the wavenumbers) for each couple of values (Cfl,Peh). You will see for example in the explicitly Euler scheme that for lower Peh you need lower Cfl to stay within the stability region. Finally, the amplifcation factor Gnum is not representing dissipation or diffusion. When compared to Gphys, if you see that Gnum introduces more diffusion than the physical one present in Gphys you deduce the presence of numerical diffusion. |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
|
Thanks professor I agree!.
Any reference you could uggest to understand and learn more about the Spectral methods and the type of techniques used for these type of analysis. Finally, to implement the equation I mentioned above, can I just use the FFT and compare it with the analytical solution? Thanks |
|
|
|

|
|
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
Julio you don't need of a real spectral method or an FFT routine. Just consider what is the process in the von Neumann stability, that is write the discrete scheme, insert the generic Fourier component and, by hand, express the amplification number. In the 1D case, this latter is a function of the variables (Cfl, Peh, k). So, you can get what you want, you can represent the surface Gnum=1 in the 3D space using Tecplot or you can represent its projection on the (Cfl,Peh) plane. A good software I used to do the whole process is Maple. |
||
|
|

|
||
|
|
|
#7 |
|
Senior Member
|
Thanks Professor, I was to focused on the equation shown above. I'll do the homework and hope to finally fully understand the Von Neumann stability criteria.
|
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
||
|
|

|
|
|
|
|
#9 | |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 15  |
Quote:
https://nptel.ac.in/courses/101104013/15 https://books.google.co.in/books/abo...EC&redir_esc=y I believe this analysis needs some more improvement to match the analysis with numerical results. I hope they will improve it. Though this numerical analysis needs improvement, it is better than other similar numerical analysis exist like spatial-DRP analysis or temporal-DRP analysis. For me, the spatial-DRP analysis does not make any sense on any PDE with finite time integration schemes but you can find a lot of papers based on spatial-DRP analysis or optimization on top tier journals even after the establishment of space-time DRP analysis. I'm personally not a fan of existing spectral analysis (known to me) applied on non-linear equation but for linear equations under some conditions they are fine. If you wish, you can share your conclusion. Thank you. |
||
|
|

|
||
|
|
|
#10 |
|
Senior Member
|
Thank you very much. I do have that textbook, but the analysis shown in the textbook is for the heat equation. Also, the process is not clear and my objective is to fully grasp the procedure.
I'll check the video lectures, thank you very much for the contribution. |
|
|
|

|
|
|
|
|
#11 | |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 15  |
Quote:
For linear convection equation, it can predict whether the solution will grow or damp but it may have some problem when the solution is having multiple wave number. I personally don't agree with the linear spectral analysis of RK methods. If you like it, you can improve this analysis. I have carried a small case study on this analysis. If you want, I can share that. I need your email, that you may share through message. |
||
|
|

|
||
|
|
|
#12 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
A discussion about the original von Neumann stability analysis and the different approach that the authors adopt in those studies was discussed also here https://www.researchgate.net/post/Ha...ory_a_flawness |
||
|
|

|
||
|
|
|
#13 |
|
Senior Member
|
Thank you very much. I'll greatly appreciate. Although I need to do my homework with the Von Neumann stability analysis, as suggested by professor Denaro. However, I'll be happy to jump onto your work to see it from your own perspective.
Julio juliocesarmendez.carvajal@gmail.com jcmendez@aggies.ncat.edu |
|
|
|

|
|
|
|
|
#14 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
I agree that the real analysis requires to take into account the full time-space discretization. In other words, the guideline for the analysis is the modified PDE induced by the full discretization. It would be interesting to analyse the modifed equation in the wavenumber space. |
||
|
|

|
||
|
|
|
#15 | |
|
Senior Member
|
Quote:
Interesing point, why such conclusion, If you do not mind to elaborate a little bit more. I'd say this paper also touches base on DRP issues since the physical speed of convection and group velocity used in the paper come from the expression valid for DRP. Without being an expert in the field, I'd say this method is very well backed up since each numerical scheme has its own analytical physical amplification factor. In fact, the paper uses different temporal and spatial schemes and at least for me, the procedure seems to be valid with no flaws at all. however, I may be overlooking something that is not obvious and I'll be happy to read your opinion. Thanks Julio |
||
|
|

|
||
|
|
|
#16 | |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 15  |
Quote:
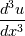
|
||
|
|

|
||
|
|
|
#17 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
When you compare the exact and the numerical solution you should be aware that: - this is the discretization error but the order of accuracy of a scheme is defined by means of the local truncation error. - the discretization error requires theo know the exact solution that, in general, is not always known. Conversely, we could always deduce the local truncation error and, this way, the modified PDE. - The modified PDE has infinite terms, if the solution is smooth you can focus only on the leading term. But in a practical computation we do not discretize the modified PDE, no matter of a kind of discretization of higher derivative |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| recommended book to the study of reaction diffusion convection equation? | lfgmarc | Main CFD Forum | 1 | January 14, 2011 07:34 |
| convection, diffusion, dispertion, advection ? | vijesh joshi | Main CFD Forum | 14 | March 18, 2006 00:20 |
| diffusion convection compressible flow | Gijs | Main CFD Forum | 0 | September 27, 2005 10:33 |
| ONLINE: literature on IMPLICIT FINITE DIFFERENCE METHODS | Yogesh Talekar | Main CFD Forum | 3 | July 28, 1999 10:54 |
| Diffusion / convection | I. Dotsikas | Main CFD Forum | 2 | April 21, 1999 17:39 |