 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Delhi
Join Date: Jul 2017
Posts: 10
Rep Power: 9  |
Hello everyone!
I am slightly confused about the validity of the law of temperature. I tried to go over literature and I couldn't find a concrete answer. I was wondering if the law of wall for temperature shifts when we can change the wall temperature. I ran RANS simulations in an in-house code for a flat plate case with different wall temperature (isothermal boundary condition). I selected Twall/Tfreestream as 1.03, 1.04, 1.05, 1.1. I observed that T+ vs y+ was varying for both SA and k-w SST turbulence models. I wondering if anyone ran a similar simulation in any other code. I want to check if this behavior is expected or not. It would be great to have the opinion of the CFD community about it. Thank you very much |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Delhi
Join Date: Jul 2017
Posts: 10
Rep Power: 9  |
It would be great if someone could give me their opinion regarding it from their experience or relevant literature.
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Lane Carasik
Join Date: Aug 2014
Posts: 692
Rep Power: 15  |
||
|
|

|
|
|
|
|
#4 |
|
Senior Member
|
Also, show us what you mean by varying (some plots would be useful), how did you define your T+ and y+, your grid parameters, what other bc you used for your case, the properties you used (are you sure the Pr number is the same?).
As it is not expected in general, the first thing I can think of is that your grid is in a gray area, and as you changed the temperature difference, the y+ range chenaged as well. You should be aware that these WF are not perfect, they typically have some variability if you change your y+. |
|
|
|

|
|
|
|
|
#5 | |
|
New Member
Delhi
Join Date: Jul 2017
Posts: 10
Rep Power: 9  |
Quote:
Keeping this un-necessary discussion aside. Can you please give any technical advice to my question? Thank you! 
|
||
|
|

|
||
|
|
|
#6 | |
|
New Member
Delhi
Join Date: Jul 2017
Posts: 10
Rep Power: 9  |
Quote:
I defined my variables as:  where, I take  is the freestream value of viscosity. is the freestream value of viscosity. where  and  is the wall temperature, is the wall temperature,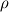 and u are freestream density and velocity respectively. and u are freestream density and velocity respectively. 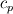 is specific heat at constant pressure and is specific heat at constant pressure and  is wall heat flux. is wall heat flux.I should mention that this dependence on wall temperature is not due to the absolute value of Twall but the difference with the freestream temperature (  ). For low temperature difference, this behavior is obtained which I find weird as most of the experimental data were obtained with low temperature difference so as to do a constant parametric (with respect to T) measurements. ). For low temperature difference, this behavior is obtained which I find weird as most of the experimental data were obtained with low temperature difference so as to do a constant parametric (with respect to T) measurements.The results are shown as follows and can be found here: https://drive.google.com/file/d/1wma...ew?usp=sharing Note that here Twall = 1.03 in the legend is basically Twall = 1.03*T_freestream. Where T_freestream is 300 K for all the simulations. The prandtl number (=0.71) and c_p are constant with temperature. These are not wall function simulations, they are low-Reynolds number turbulence model simulations with y+ < 0.1. I did mesh convergence study and the result is not varying. It is important to tell here that the U+ vs y+ profile is almost identical to the analytic one for all wall temperatures. I understand your point about grid variability, however I am not running wall functions. It's the turbulence model solved to the wall with y+ < 0.1. The BC I used for the wall is isothermal wall. The case is exactly the 2-D flat plate case in NASA turbulence modeling resource. Unfortunately, they don't provide heat transfer data for validation. The velocity profile shows good agreement with CFL3D data. |
||
|
|

|
||
|
|
|
#7 |
|
Senior Member
|
Let us assume that you are computing a constant density flow, otherwise things get much more involved (or, in any case, let us assume that density variations are negligible).
Let us also assume that the viscosity variation with temperature is negligible, as this is the case under which classical law of the walls actually hold. In this scenario, your definition of  seems wrong to me, as it requires the local seems wrong to me, as it requires the local  and not freestream value of u at the denominator. and not freestream value of u at the denominator.Second, how do you compute 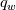 ? ?In any case, my experience is with the channel flow where, using a temperature bc instead of a fixed flux one, I also experienced non collapsing profiles, but that was for different Re numbers, which might be a different scenario. |
|
|
|

|
|
|
|
|
#8 |
|
New Member
Delhi
Join Date: Jul 2017
Posts: 10
Rep Power: 9  |
Quote:
 is indeed as follows, is indeed as follows, I computed  as as 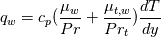 from the CFD solution where from the CFD solution where 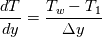 where where  is the temperature at the first cell and is the temperature at the first cell and 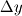 is the wall distance. I checked my Stanton number results and they match with the empirical solutions. So, I guess is the wall distance. I checked my Stanton number results and they match with the empirical solutions. So, I guess  computation (even though it is first order), is not the reason. I also tried green-gauss to get the value of temperature gradient, however, results are still the same. Hmm, I realised that I am using viscosity at the wall for computation (even though it is first order), is not the reason. I also tried green-gauss to get the value of temperature gradient, however, results are still the same. Hmm, I realised that I am using viscosity at the wall for  computation. This seems correct with the physics! computation. This seems correct with the physics!
Last edited by aviral2000; March 29, 2019 at 12:39. |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
|
Everything seems legit to me. As I said, I found a similar behavior when changing the Re number, for fixed wall temperature, in a periodic channel flow. Maybe the two things are related.
Yet, the fact that it gets worst with decreasing temperature difference, which is at your T+ numerator, is suspicious... maybe there is a utau dependence from the temperature difference? |
|
|
|

|
|
|
|
|
#10 | |
|
New Member
Delhi
Join Date: Jul 2017
Posts: 10
Rep Power: 9  |
Quote:
Hmm, I don't think that there is 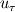 dependence as the velocity profile and skin-friction results matches perfectly. As of the current moment, my guess is the computation of dependence as the velocity profile and skin-friction results matches perfectly. As of the current moment, my guess is the computation of  is not accurate or probably for the specified conditions i.e. Mach number (0.2 in my case), this behavior is expected. I am testing other mach numbers to understand this behaviour. I expect the is not accurate or probably for the specified conditions i.e. Mach number (0.2 in my case), this behavior is expected. I am testing other mach numbers to understand this behaviour. I expect the  to change slightly with Mach number. Do you think this is expected? to change slightly with Mach number. Do you think this is expected?Thanks for suggestions. 
|
||
|
|

|
||
|
|
|
#11 | |
|
New Member
Delhi
Join Date: Jul 2017
Posts: 10
Rep Power: 9  |
Quote:
 i.e. at higher Eckert number, the viscous dissipation is significant enough to affect the temperature distribution in the boundary layer. I initially found it strange as I am still within the subsonic regime (M = 0.2) when I observe the deviation in the temperature profile. The reason my Stanton number distribution matched nicely with empirical results is that I was using the following definition, i.e. at higher Eckert number, the viscous dissipation is significant enough to affect the temperature distribution in the boundary layer. I initially found it strange as I am still within the subsonic regime (M = 0.2) when I observe the deviation in the temperature profile. The reason my Stanton number distribution matched nicely with empirical results is that I was using the following definition, where where 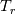 is the adiabatic wall temperature. The use of this definition makes my Stanton number distribution quite independent of Mach number, however, the temperature distribution in the boundary layer is still affected. is the adiabatic wall temperature. The use of this definition makes my Stanton number distribution quite independent of Mach number, however, the temperature distribution in the boundary layer is still affected. At lower mach number (M = 0.1), the T+ vs y+ curve for different wall temperature were matching perfectly. I also tried removing the viscous dissipation term from the RANS solver and observed that even though my St number result is different now (expected behaviour), the temperature profile for different mach numbers are matching nicely. Most of the T+ vs y+ curves and studies are for incompressible solver which does not model viscous dissipation term. Also, for higher compressible flows, Van-Driest or other similar transformations are used to convert to velocity and temperature profile to analytic ones. The case I was doing was in sort of a gray area as I was using a compressible solver for a low-speed flow without using these transformations for the velocity profile. That's my opinion regarding the issue. It will be great to have an opinion from you and other members of CFD community regarding it. Feel free to point out any mistakes in my reasoning or suggestions for additional verification tests. Thank you! 
|
||
|
|

|
||
|
|
|
#12 | |
|
Senior Member
|
Quote:
In more general terms, I would conclude that the main mistake was in applying an incompressible law to a compressible case. Thus, besides the viscous dissipation term, a varying density and, in case, viscosity, might invalidate it as well. |
||
|
|

|
||
 |
| Tags |
| heat transfer, law of wall, temperature, turbulence modeling |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Wall treatment with OpenFOAM | roby | OpenFOAM Running, Solving & CFD | 48 | May 28, 2021 12:38 |
| [Commercial meshers] Fluent3DMeshToFoam | simvun | OpenFOAM Meshing & Mesh Conversion | 50 | January 19, 2020 16:33 |
| Centrifugal fan | j0hnny | CFX | 13 | October 1, 2019 14:55 |
| velocity BC for pourous wall (pressure dependendend darcy law) | StefanW | OpenFOAM Running, Solving & CFD | 1 | May 29, 2017 08:53 |
| Wall Function Approach - log law | Paul | CFX | 2 | June 30, 2005 07:06 |