 |
|
|
[Sponsors] | |||||
discretization of convective terms of Spalart Allmaras equations |
 5Likes
5Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Abolfazl
Join Date: Oct 2016
Posts: 28
Rep Power: 10  |
Hi everyone.
I'm about to discretize the spalart allaras equation and add it into my compressible code based on Roe scheme. I was wondering can i use a simple first or second upwind for discretization of convective terms of spalart allmaras like incompressible flow or I should use the method of Roe!? thanks a lot |
|
|
|

|
|
|
|
|
#3 | |
|
New Member
Abolfazl
Join Date: Oct 2016
Posts: 28
Rep Power: 10  |
Quote:
Actually I don't know. I know how i can use forward and backward discretization for convective term of spalart and this is all I know. I have no idea how I can use Roe for spalart! actually maybe I'm not asking the right question. I'm not well familiar with turbulence models. |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
|
Well, I tougth that, as you have a Roe scheme in your compressible code, you kind of knew it. For a general vector equation of the form:
 your Roe scheme for the flux  at the interface between cells L and R typically is: at the interface between cells L and R typically is:![\textbf{F} = \frac{1}{2}\left[\textbf{F}\left(\textbf{W}_L\right)+\textbf{F}\left(\textbf{W}_R\right)-\textbf{M}\left|\Lambda\right|\textbf{M}^{-1}\left(\textbf{W}_R-\textbf{W}_L\right)\right] \textbf{F} = \frac{1}{2}\left[\textbf{F}\left(\textbf{W}_L\right)+\textbf{F}\left(\textbf{W}_R\right)-\textbf{M}\left|\Lambda\right|\textbf{M}^{-1}\left(\textbf{W}_R-\textbf{W}_L\right)\right]](/Forums/vbLatex/img/f35a218f19ec670457d02a4a986cabae-1.gif) where:  is the Jacobian of the flux (upwind altered by taking the absolute eigenvalues), the surface normal is assumed to point toward the R cell and the L and R states can be, in general, cell values (1st order) or suitably reconstructed values (2nd or higher order). Now, if you apply this to a scalar equation for 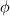 with assigned mass flux, say with assigned mass flux, say  , which is the first component of , which is the first component of  above, you get as flux: above, you get as flux:![F = \frac{1}{2}\left[m\left(\phi_L+\phi_R\right)-\left|m\right|\left(\phi_R-\phi_L\right)\right] F = \frac{1}{2}\left[m\left(\phi_L+\phi_R\right)-\left|m\right|\left(\phi_R-\phi_L\right)\right]](/Forums/vbLatex/img/bb591db1c63fb87bf924c329d88b2b99-1.gif) which actually is the upwind scheme in its most common version. In layman's terms, the point is that, for a scalar equation, you don't have a wave structure anymore, just a single eigenvalue,  . .
|
|
|
|

|
|
|
|
|
#6 | |
|
New Member
Abolfazl
Join Date: Oct 2016
Posts: 28
Rep Power: 10  |
Quote:
thank you for your kind reply. I checked the "computational fluid dynamics Vo.II" written by Hoffmann. I found that I can discrete the convective terms using a simple upwind scheme. but now I have another question. there is a term in Spalart Allmaras model:  ? ?I know 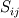 is is  but I don't get it how i can expand but I don't get it how i can expand  ! !is the expansion for 2D like this?  ? ?How like is the expansion for 3D? thanks a lot! Last edited by Abolfazl_cfd; April 7, 2019 at 14:01. |
||
|
|

|
||
|
|
|
#7 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,877
Rep Power: 73    |
Quote:
No, Sij is the symmetric part of the velocity gradient. But what is more, stands in that fact the a turbulence model for incompressible flows does not necessarily can be extended as it is to compressible flows. Have a look here http://iccfd.org/iccfd7/assets/pdf/p...1902_paper.pdf |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Unless you absolutely need to use the Roe scheme, I would suggest the AUSM+ scheme (or one of the variants.) It's easier to implement, cheaper in computational cost, and can be more accurate than the Roe scheme (I can't think of a case of where it's not.)
|
|
|
|

|
|
|
|
|
#9 | |
|
New Member
Abolfazl
Join Date: Oct 2016
Posts: 28
Rep Power: 10  |
Quote:
Thank you for correcting my mistake. I toke a look into the paper and found it really helpful. specially the part about negative values of source term in Spalart Allmaras. Thank U. |
||
|
|

|
||
|
|
|
#10 | |
|
New Member
Abolfazl
Join Date: Oct 2016
Posts: 28
Rep Power: 10  |
Quote:
Thank you for your precious advice. Actually I am working on immersed boundary method. years ago I tried to add my immersed code to a AUSM solver but some instabilities near the immersed boundary started to grow and after several attempts I gave up upon AUSM. But for Roe scheme it works properly. Thanks a lot. |
||
|
|

|
||
|
|
|
#11 | |
|
New Member
Abolfazl
Join Date: Oct 2016
Posts: 28
Rep Power: 10  |
Quote:
finally I could write the spalart allmaras code. Although instead of Roe scheme, I used E-CUSP scheme, but the results in channel flow in Re=10000 are satisfactory. If anyone need the code, can send me an email. I would happy to share it and I hope it would help. moosavi.abolfazl@gmail.com |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| A problem about using the Spalart Allmaras model | shiningkissss | CFX | 4 | April 23, 2017 23:28 |
| CFX Spalart Allmaras turbulence models | aweizazuji | CFX | 9 | September 24, 2013 11:53 |
| Spalart Allmaras Paper | Seroga | Main CFD Forum | 0 | April 7, 2008 03:48 |
| About discretization equations for Axisymmetric | Dalitj | Main CFD Forum | 0 | August 15, 2003 00:50 |
| Turbulent terms in the MRF equations | Francisco Saldarriaga | Main CFD Forum | 1 | July 22, 1999 17:49 |