[lucamirtanini]

Hi,

I have several doubts on the correlation tensor component on the diagonal:

1. I have tried to calculate my correlation functions of a buoyant plume.
I have the velocity component recorded at a time step of 0.001 s, so starting from this formula

Rii (r) =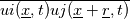
Since the overbar should be a time averaging, as stated by Tennenkes, i can write it:
Rii (r)= lim 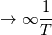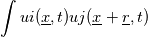T dt
Moreover, provided that T is large enough, I can use the summation operator
Rii (r)= 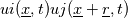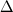T

Is this approach correct? I have some colleagues that are telling me that in their opinion the overbar is a spatial average and that this calculation should be done at a fixed time step. That's why I am asking

2. As you can see in the file uploaded, Tennekes and Lumley have shown two examples of correlation function. Do you think that their trend that they have drawn is typical, or just casual? I have tried to plot mine, but they are really different from the ones of the Tennekes book, as you can see in the attached file

[FMDenaro]

Yes, it is assumed that the time is fixed and the averaging is over the x direction so that the correlation is a function only of the separation r

[lucamirtanini]

Originally Posted by FMDenaro

Yes, it is assumed that the time is fixed and the averaging is over the x direction so that the correlation is a function only of the separation r

Thank you for your reply, but I have not understood your answer! Do you think that I should not time averaging?
Is the overbar a time averaging?
Why are you talking of x direction

[FMDenaro]

Originally Posted by lucamirtanini

Thank you for your reply, but I have not understood your answer! Do you think that I should not time averaging?
Is the overbar a time averaging?
Why are you talking of x direction

You are wrong, the expression of the Rii you wrote is a spatial correlation (see x and x+r) not a time correlation. Therefore it is assumed to perform the correlation operation at a certain time t. The overbar is the statistical mean and under suitable properties (ergodicity) the spatial and time averaging do converge towards the same mean

[LuckyTran]

What you wrote is a spatial correlation (because x and x+r) and the overbar is averaging in time.


There is also a temporal correlation (where you'll find instead t and t+r).


To calculate the spatial correlation you need to measure velocity at all x (i.e. an entire line) for all time. If you measure velocity only at a single point, you won't be able to calculate the spatial correlation function.

[lucamirtanini]

Thank you for your reply. Unfortunately I am still confused. If I follow the Tennekes book, the overbar is defined as a time average (page attached).

I think I ve explained badly. I ve placed 70 velocity device along the z axis (in the centerline of my domain), so I have decided that this axis define the direction of my separating vector r.

So I have done the correlation between these velocity component, but I have done a time average.

I do not understand if this procedure is right, or if I should have placed other velocity device in order to do a spatial average. Unfortunately I cannot find reference for the detail of this calculation

[FMDenaro]

The overbar stands in general for a statistical mean like an ensemble averaging. Under particular assumption, this averaging as the same convegence of the time ans spatial averaging. However, the key is that you have to consider the separation r in space along x. Of course, if you have for example measurements in a plane of homogeneity of the flow, you can repeat this procedure along x at the others location in the plane (z direction). Then the overbar is performed by the time averaging and the spatial averaging along z

[lucamirtanini]

Originally Posted by FMDenaro

The overbar stands in general for a statistical mean like an ensemble averaging. Under particular assumption, this averaging as the same convegence of the time ans spatial averaging.

When you say ensamble averaging, are you meaning a generic mean in time or space?

Originally Posted by FMDenaro

However, the key is that you have to consider the separation r in space along x. Of course, if you have for example measurements in a plane of homogeneity of the flow, you can repeat this procedure along x at the others location in the plane (z direction). Then the overbar is performed by the time averaging and the spatial averaging along z

So was my procedure right?

I multiplied the velocity components recorded at different location along the separating vector (as indicated in the formulae that I have shown), at the same time step, and then I have time averaged.
When you are talking about ensamble average are you meaning that there is not difference between time averaging or space averaging?

[FMDenaro]

The meaning implied by the overbar operation is as same as that implied in the RANS equations, just consider that at r=0 the correlations are the entries of the unresolved Reynolds tensor.

[lucamirtanini]

Originally Posted by FMDenaro

The meaning implied by the overbar operation is as same as that implied in the RANS equations, just consider that at r=0 the correlations are the entries of the unresolved Reynolds tensor.

I have not understood if your answer means yes or no

[FMDenaro]

You did a time-averaging, that is correct for statistically steady and homogeneous flows for which ergodicity can be invoked.
There is not a unique definition for the overbar operation in defining RANS eqs.

[lucamirtanini]

I am not using a RANS model, but a LES.

It is a statistically steady flow, but not homogeneous.

In the Tennekes book there is not an other explanation of the overbar, it is always defined as time averaging. Btw I cannot understand, in my case study, the sense of doing a spatial average in a flow like a buoyant plume, where there is not a defined domain like in a pipe, where the pipe defines the boundary of the flow. In this case is not easy to define in which point should I place the velocity device, since in certain points the velocity is almost 0.

[lucamirtanini]

https://nptel.ac.in/courses/11210411...elation_fn.htm

Also in these slide, it is assumed a time averaging.

[LuckyTran]

So you have velocity at 70 different locations and many many time-steps right (let's say 1000 time-steps)?

At every time-step, you should do the sumproduct of the velocity with the velocity shifted by r (start with 0). Then you average over the 1000 time-steps. This gifts you Rij at r=0.

Then you shift by r=1. Take the sumproduct again. Average all 1000 again. This gives you Rij(r=1).

Repeat until you exhaust all the r's.

Again, this is the arithmetic way to do it which is in my opinion the best way for you to learn how to do it right now. Eventually you'll learn to abuse the Fourier properties and use the fft for large datasets.

This is how you get the spatial correlation. Temporal correlation (which has almost the exact same formula but you swap x with t) is done the other way around.

Originally Posted by lucamirtanini

It is a statistically steady flow, but not homogeneous.

In the Tennekes book there is not an other explanation of the overbar, it is always defined as time averaging. Btw I cannot understand, in my case study, the sense of doing a spatial average in a flow like a buoyant plume, where there is not a defined domain like in a pipe, where the pipe defines the boundary of the flow. In this case is not easy to define in which point should I place the velocity device, since in certain points the velocity is almost 0.

What you say is correct. The spatial correlation will be dependent on where you put your velocity measurement devices. This is not wrong, because Rij is a function of x and r. The x here is the reference location you take for your spatial correlation. Only in the case of homogeneous turbulence does the spatial correlation become degenerate and is the same at all locations.

[FMDenaro]

Originally Posted by lucamirtanini

I am not using a RANS model, but a LES.

It is a statistically steady flow, but not homogeneous.

In the Tennekes book there is not an other explanation of the overbar, it is always defined as time averaging. Btw I cannot understand, in my case study, the sense of doing a spatial average in a flow like a buoyant plume, where there is not a defined domain like in a pipe, where the pipe defines the boundary of the flow. In this case is not easy to define in which point should I place the velocity device, since in certain points the velocity is almost 0.

That is exactly what stated at page 28 in the textbook of Lumley to introduce the time-averaging. You will get the dependence of the correlation function on the position owing to the inhomogeneity of your flow problem. But you are safe if the problem is statistically steady.

To see more about the types of averaging and their properties, I suggest to have also a look to the book of Wilcox.

[lucamirtanini]

Originally Posted by LuckyTran

So you have velocity at 70 different locations and many many time-steps right (let's say 1000 time-steps)?

At every time-step, you should do the sumproduct of the velocity with the velocity shifted by r (start with 0). Then you average over the 1000 time-steps. This gifts you Rij at r=0.

Then you shift by r=1. Take the sumproduct again. Average all 1000 again. This gives you Rij(r=1).

Repeat until you exhaust all the r's.

Again, this is the arithmetic way to do it which is in my opinion the best way for you to learn how to do it right now. Eventually you'll learn to abuse the Fourier properties and use the fft for large datasets.

This is how you get the spatial correlation. Temporal correlation (which has almost the exact same formula but you swap x with t) is done the other way around.

What you say is correct. The spatial correlation will be dependent on where you put your velocity measurement devices. This is not wrong, because Rij is a function of x and r. The x here is the reference location you take for your spatial correlation. Only in the case of homogeneous turbulence does the spatial correlation become degenerate and is the same at all locations.

Thank u for your answer. I am doing exactly like you said. So I am very happy.
Of course, I am doing this as training. Also because I have no background about signal processing, I am learning it. Do you have a good reference book for signal processing to recommend?

[lucamirtanini]

Originally Posted by FMDenaro

That is exactly what stated at page 28 in the textbook of Lumley to introduce the time-averaging. You will get the dependence of the correlation function on the position owing to the inhomogeneity of your flow problem. But you are safe if the problem is statistically steady.

To see more about the types of averaging and their properties, I suggest to have also a look to the book of Wilcox.

Thank u. also for the recommerndation