[Vignesh2508]

Hi Guys,


I have two questions:


1. I usually do unsteady transient analysis using an explicit scheme respecting the CFL condition. But my professor asked me to use an Implicit time stepping scheme. This has given me a lot of doubts. The implicit scheme is unconditionally stable in theory. So should I mind the CFL condition here. Because using large CFL number in the order of thousands will skip a lot of grid cells and ignore information in between leading to non-sensical solutions. Can anyone clarify this?


2. Is CFL condition applicable to all fluid flows (omnipotent?). I am doing bluff body simulations. Is CFL condition applicable to all bluff body flows (aside from explicit and implicit debate).


(PS: Is CFL number and Courant number one and the same? If so why different way of calling?)



Thanks


Vignesh

[GregCFD]

1. Unconditionally stable doesn't mean unconditionally accurate, just because the solution doesn't diverge doesn't mean it's accurate. You'll still need to determine the largest timestep which will return accurate results, it's very very unlikely to be with a Courant number in thousands for the reasons you gave.

2. Yes? The CFL condition is a restraint that is necessary for convergence of explicit methods. If your asking if you can use the same Courant number for all flows then the answer is not for implicit methods, you might find a solution it time accurate with C = 2 or C = 20.

CFL vs Courant Number) They are generally seen as the same thing, more correctly one is a condition, the other is a dimenionless number and it's probably a good idea to distinguish the two.

Courant Number (C) is the dimenionless number defined as (in 1D)
C= dt*U/dx;

(CFL) is for Courant, Friedrichs, & Lewy, it's the condition that must be satisfied for convergence in explicit methods.

C < C(max)

[Vignesh2508]

1. To determine the largest time step for a time accurate result with implicit scheme, one has to conduct a time sensitivity study (this sounds like a trial and error method), right?


2. In the Courant number, is the velocity considered for estimation free stream velocity or something else? I have come across some post saying that the velocity used in the courant number calculations has to be 50% of the free stream velocity. If we use the free stream velocity then it is a conservative estimate. Is this true?



Thanks


Vicky

[LuckyTran]

I would add that an implicit scheme being unconditionally stable is for a very specific choice of discretization in time and space and for a very specific governing equation with very specific boundary conditions. Unless you say specifically what all of these are, you cannot say "oh look, using an implicit time-stepping scheme guarantees my solution is stable." Usually this holds only for the simplest 1st order backward time.

Yes, using a very large time-step will cause inaccuracies because information will skip cells. Some schemes are naturally inaccurate, 2nd order backward Euler for example produces overshoots and undershoots (which is completely wrong).

Also, you assume you can even do a fully implicit time-stepping procedure, which you often can't if you have a energy equation coupled to the momentum + continuity equation (because there is a kinetic energy term that looks like U^2 that can only be computed explicitly, otherwise you have a closure problem).

There is not one kind of Courant number because the speed that goes into the Courant number is the speed of propagation of disturbance (which is not always a velocity disturbance, because you could be talking about a temperature disturbance, or some other physics). For compressible flows the Courant number must also take the into account the speed speed and so on. Finally, the Courant number is a field and not a single value for the entire domain. The Courant number also changes with the solution in time and there is not a fixed Courant number for all time. The Courant number is just a non-dimensionalized solution speed.

So yes. There is trial and error method to determine largest time-step for a desirable amount of accuracy. And accuracy is quite subjective and depends what type of information you are trying to get.

Originally Posted by Vignesh2508

1. To determine the largest time step for a time accurate result with implicit scheme, one has to conduct a time sensitivity study (this sounds like a trial and error method), right?

Yes, always. Unless you've done it before, in which case you've already done the trial.

Originally Posted by Vignesh2508

In the Courant number, is the velocity considered for estimation free stream velocity or something else? I have come across some post saying that the velocity used in the courant number calculations has to be 50% of the free stream velocity. If we use the free stream velocity then it is a conservative estimate. Is this true?

The Courant number is a field that uses always the local speed and local length scale (cell size). You need to distinguish between what this actual field is, and how to guess what is the maximum Courant number of this field. Most people are doing the latter when they talk about Courant number.

You use the freestream velocity because often the freestream velocity is the maximum velocity and this let's you quickly estimate the maximum Courant number. Of course this is only for very simple kindergarden problems (because flows can accelerate around bodies and you can easily find velocities greater than the maximum velocity). And then they take 50% to try to be conservative. But this is because they are guessing in the dark at what the maximum Courant number is in this Courant number field which they have not yet computed.

If you want to know what the Courant number field is, you have to do the trial-and-error, get a solution and calculate the actual Courant number. People spend wayyyy too much effort talking about how to guess the Courant number rather than just brute-forcing it. It's not that complicated.

[FMDenaro]

In a real 3D simulation of viscous flows, one must be aware of what we define as CFL number (local and 3D) and, in terms of numerical stability, the CFL is strictly linked to the viscous stability parameters.
Explicit scheme are always stable? It depends on the global discretization and do not forget that the stability analysis is performed in the linear framework.
Finally, for transient physics, you should see the physical characteristic time. That means that, no matter of explicit or implicit method, you are required to use the proper time step.
If you are interested only in a steady solution, the explicit method can give some adantage.

[Vignesh2508]

Originally Posted by FMDenaro

Explicit scheme are always stable? It depends on the global discretization and do not forget that the stability analysis is performed in the linear framework.

You meant to say Implicit scheme right? Because for non-linear problems implicit scheme is not always stable.

Originally Posted by FMDenaro

If you are interested only in a steady solution, the explicit method can give some adantage.

I thought for a steady solution implicit method is the go to one, as there is no meaning for the time step.

[Vignesh2508]

Originally Posted by FMDenaro

The Courant number is a field that uses always the local speed and local length scale (cell size). You need to distinguish between what this actual field is, and how to guess what is the maximum Courant number of this field. Most people are doing the latter when they talk about Courant number.

You use the freestream velocity because often the freestream velocity is the maximum velocity and this let's you quickly estimate the maximum Courant number. Of course this is only for very simple kindergarden problems (because flows can accelerate around bodies and you can easily find velocities greater than the maximum velocity). And then they take 50% to try to be conservative. But this is because they are guessing in the dark at what the maximum Courant number is in this Courant number field which they have not yet computed.

We need to first do a trial simulation to estimate the Courant field. And to do that simulation we estimate a maximum Courant number. The flow field will mostly have a minimum grid size near the boundary layers, and the flow velocity considered in that region will be lower and sometimes significantly lower than the free stream velocity. Considering free stream velocity in that situation is being too much conservative right? As you said these issues can be averted by bruteforcing which can be done later.

[FMDenaro]

Originally Posted by Vignesh2508

You meant to say Implicit scheme right? Because for non-linear problems implicit scheme is not always stable.

I thought for a steady solution implicit method is the go to one, as there is no meaning for the time step.

Sorry, I actually wrote explicit while thinking implicit

[FMDenaro]

Originally Posted by Vignesh2508

We need to first do a trial simulation to estimate the Courant field. And to do that simulation we estimate a maximum Courant number. The flow field will mostly have a minimum grid size near the boundary layers, and the flow velocity considered in that region will be lower and sometimes significantly lower than the free stream velocity. Considering free stream velocity in that situation is being too much conservative right? As you said these issues can be averted by bruteforcing which can be done later.

Well, the things in a real 3D case are quite more complex. As an example, if you use the calssical FTUS scheme in a 3D case, the CFL number for the stability is actually the sum of the three CFL in each direction. That means you have to consider the most critical situation in which f=(u/dx +v/dy +w/dz) has the maximum value. Then dt<=1/f_critical.
But if you mix this analysis with the discretization of the diffusive terms you have to consider the hypersurface CFL(Re_dx,Re_dy,Re_dz).

[Vignesh2508]

I was talking with my professor and he was of opinion that Courant number is only for high speed flows. There is no need to apply it for Incompressible flows (we had an argument about this). My Reynolds number is in the range of 10^5.

[FMDenaro]

Originally Posted by Vignesh2508

I was talking with my professor and he was of opinion that Courant number is only for high speed flows. There is no need to apply it for Incompressible flows (we had an argument about this). My Reynolds number is in the range of 10^5.

That is not true, the CFL condition makes physical sense in any highly non linear flow phenomenon.

[sbaffini]

A kind of definitive source on this is the book by Blazek (see pages 175-176 more specifically):

https://books.google.it/books?id=r-e...ctured&f=false

The basic idea is that, very roughly speaking, your variable update has the general following form: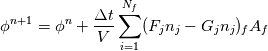



So you set up your local max time step according to: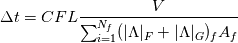



This is actually very conservative however