 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Jun 2017
Posts: 24
Rep Power: 9  |
 I'm working with a finite volume scheme to solve the shallow water equations on a 2d flow. However, I'm having issues understanding the boundary conditions. I'm working with a finite volume scheme to solve the shallow water equations on a 2d flow. However, I'm having issues understanding the boundary conditions.So far, I think I understand that the condition at the wall can be either non slip, or slip. I don't know however when the slip condition can be applied. At the same time I know that a boundary can be reflective or transmissive? (I know there are many more possibilities, but for now I'm focused on these cases). My question is, for a 2d case if I want to put a reflective boundary, then I should fix the normal velocity of the next cell (beyond the domain) equal to the one of the last cell within the domain, right? If that is the case, then what should I fix for the tangential velocity? Because I'm using an explicit scheme, I need a value for the tangential velocity also. Does this value depend either on a non slip or a slip condition? Then the boundary is reflective and non slip? Or just the reflective boundary condition involves fixing also the tnagential velocity to some value? |
|
|
|

|
|
|
|
|
#2 |
|
Super Moderator
|
If you have a first order problem like inviscid flow, you can only say that normal velocity must be zero because the fluid cannot penetrate into a solid wall, so there can be tangential or slip velocity.
For second order (parabolic) problem like navier-stokes, the full velocity must be zero at a stationary wall, which is called no-slip condition. Reflective boundary is used as a synonym for slip boundary. For slip boundary: assuming you are using a cell-centered formulation, i.e., your first grid point is above the wall, you can set the velocity in the ghost cell by reflecting the normal component and the tangential component is unchanged. So if  is velocity vector at first cell, then you set is velocity vector at first cell, then you set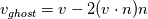 where 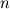 is the normal vector to the boundary. is the normal vector to the boundary.
|
|
|
|

|
|
|
|
|
#3 |
|
New Member
Join Date: Jun 2017
Posts: 24
Rep Power: 9  |
Quote:
 (normal) and (normal) and  (tangential) are the components of the velocity vector (tangential) are the components of the velocity vector  , then I was setting for the ghost cell (yes, I have a cell-centered formulation): , then I was setting for the ghost cell (yes, I have a cell-centered formulation):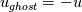 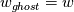 But I have a cartesian grid and with that expression, I'd only have one value of velocity, is that just for the normal component? And then the tangential, I just simply say it remains unchanged? |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
In your original question I see a mix of doubts about physical and numerical BC.s to se at a wall. 1) Physical BC.s: use the no-slip condition for real fluid where viscosity is taken into acccount. The slip condition is used for the simplified inviscid flow model (Euler equations). 2) Numerical B.C.s: if you are looking for a way to set a value in a ghost point, say at a location yh (1d example), having the value at the wall (yw) and in a set of interior nodes (y1, y2, y3,..), you have to prescribe a value that is congruent with the accuracy order of your scheme. If you have a low order scheme, no more than second order, you can use the values at yw and y1 in order to evaluate a linear law and extrapolate the value at yh. If the scheme has higher order of accuracy you need to extrapolate the value at yh using more infos, for example the value at y2 (or, when possible, the condition of the normal derivative at the wall). |
|
|
|

|
|
|
|
|
#5 | |
|
New Member
Join Date: Jun 2017
Posts: 24
Rep Power: 9  |
Quote:
Because the non slip condition actually set the normal velocity to 0, right? and the tangential one also is 0? But if I want the waves to be reflected, then I need to null normal velocity! |
||
|
|

|
||
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Reflection of a wave on a wall is a quite different issue and depends on the type of wave (acoustic, convective, ..). Generally, this aspect is relevant for the Euler equations (inviscid flow model) or for compressible Navier-Stokes equations at very high Reynolds number. There are many papers about the types of BC.s for such flow problem. One of the relevant paper is from Poinsot and Lele on JCP. |
||
|
|

|
||
|
|
|
#7 | |
|
New Member
Join Date: Jun 2017
Posts: 24
Rep Power: 9  |
Quote:
 , then at the ghost cell, I should have a , then at the ghost cell, I should have a 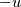 velocity, is that correct? And the same for the tangential component, velocity, is that correct? And the same for the tangential component, 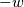 ? That way, I have non null velocities at the ghost cell, but null velocity at the boundary, for both components. ? That way, I have non null velocities at the ghost cell, but null velocity at the boundary, for both components. And the last question, for the water depth, is it correct to simply use the same water depth than the first cell within the domain (not interpolating)? |
||
|
|

|
||
 |
| Tags |
| boundary cells, boundary condition., finite volume method, shallow water equations, slip bc |
|
|