 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Javier
Join Date: Nov 2017
Posts: 6
Rep Power: 9  |
Hello everyone,
I have successfully implemented a finite-difference WENO5 2D compressible flow solver for the Euler equations in cartesian coordinates, but I'm having trouble with the generalization to curvilinear body-fitted grids. I was given a compact finite-difference solver that works fine in curvilinear grids, so my guess is that the problem may be in:
I read several articles on the matter such as this or this, but I cannot understand precisely the procedure they are using. Any help about the generalization of the global LxF splitting and/or WENO5 would be appreciated. Thank you. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 211
Rep Power: 17  |
you'd be surprised, it is not that difficult. In-fact, if you use a curve-linear solver, you don't need to change your WENO5 subroutine, it will still be used the same way for curve-linear grids. The only difference is in the discretisation of the governing equation. Lets take the divergence of the velocity field (continuity equation), for example. we have (ignoring density), in cartesian form
 . .Now to extend that to curve-linear coordinate systems, you simply need to do the coordinate transformation into a new, cartesian coordinate system, usually denoted by the new directions  and and 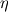 so that we have now (using the chain rule) so that we have now (using the chain rule) . .Since your derivatives of u and v are now evaluate on the new, transformed (cartesian) grid with direction of  and and 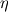 , you can use your WENO5 subroutine just like you would when using a cartesian grid. the only difficulty arises now how you get your so called metric coefficients, i.e.: , you can use your WENO5 subroutine just like you would when using a cartesian grid. the only difficulty arises now how you get your so called metric coefficients, i.e.:  (note here that the subscript just means that the derivative with respect to the subscript is taken, see also equation above). (note here that the subscript just means that the derivative with respect to the subscript is taken, see also equation above). The answer takes a bit longer and there are a couple of good books which explain that rather well (you actually have to take the so called inverse transformation, i.e. your metric coefficients are  which changes the above equation slightly (you'll end up with the jacobian of the system)). Don't worry if that seems confusing at the moment. Have a look at "Anderson, Computational Fluid Dynamics, The basics with applications (Chapter 5 (theory) and Chapter 8 (example calculation using curve linear grids) )" and "Hoffman, Chiang, Computational Fluid Dynamics for Engineers, Vol. 1 (Chapter 9)". Both are excellent references and I was able to write my own curve-linear code after consulting those two references. which changes the above equation slightly (you'll end up with the jacobian of the system)). Don't worry if that seems confusing at the moment. Have a look at "Anderson, Computational Fluid Dynamics, The basics with applications (Chapter 5 (theory) and Chapter 8 (example calculation using curve linear grids) )" and "Hoffman, Chiang, Computational Fluid Dynamics for Engineers, Vol. 1 (Chapter 9)". Both are excellent references and I was able to write my own curve-linear code after consulting those two references.
|
|
|
|

|
|
|
|
|
#3 |
|
New Member
Javier
Join Date: Nov 2017
Posts: 6
Rep Power: 9  |
Thank you very much for your reply, t.teschner. I will have a look at those books.
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
This is all true. Just be sure that your grid mapping is smooth, say from a full-domain conformal mapping. It should be at least several times differentiable. You should recognize that the WENO smoothness metrics are based on the assumption of evenly spaced samples. If the grid spacing changes in an non-smooth way, the effect of the mesh stretching will not be "felt" by the smoothness indicators, so the WENO stencils will be weighted based on incorrect data. The same is true for normal linear finite differences as well, but the potential for out-sized errors are introduced with the nonlinear behavior of WENO or limiters, etc.
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 211
Rep Power: 17  |
good point, did not consider that. thanks for adding that!
|
|
|
|

|
|
|
|
|
#6 |
|
Super Moderator
|
||
|
|

|
|
|
|
|
#7 |
|
New Member
Javier
Join Date: Nov 2017
Posts: 6
Rep Power: 9  |
Thank you very much for all your answers. I am still putting the pieces together, but I am on the correct path.
On a related note, I hope it is not off-topic, I am interested on implementing a slightly different slip wall boundary condition. Many authors mirror the flow values (i.e. density, tangent velocity and pressure) across the wall boundary (which is placed on an interface midway between nodes) and negate the normal velocity. Is there a way to make the wall boundary fall on a node instead of on an interface using WENO? The reasoning behind this is to be able to compare the results of a problem with a Finite Difference code having the nodes placed on the same coordinates. |
|
|
|

|
|
 |
| Tags |
| curvilinear, lax-friedrichs, weno5 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [OpenFOAM] Xlib: extension "GLX" missing on display | goldbeard | ParaView | 5 | March 24, 2013 14:12 |
| errors when installing openfoam2.1 on ubuntu12.o4 | hewei | OpenFOAM Installation | 5 | May 29, 2012 08:43 |
| [OpenFOAM] Saving ParaFoam views and case | sail | ParaView | 9 | November 25, 2011 16:46 |
| why low number of grids in WENO | HaKu | Main CFD Forum | 0 | April 17, 2011 03:28 |
| [OpenFOAM] Xwindows crash with paraview save | srinath | ParaView | 1 | October 15, 2008 10:37 |