 |
|
|
[Sponsors] | |||||
Is there a simple way to avoid carbuncles for FD WENO methods? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Oleg Sutyrin
Join Date: Feb 2016
Location: Russia
Posts: 41
Rep Power: 10  |
I have implemented finite-difference WENO scheme for Euler equations (with some variants - WENO-JS, WENO-Z, WENO-M, different flux splitting). It works well, but have problem with so-called carbuncles (shock instability in the areas where its front is almost aligned with the grid). This problem seems to be well-studied for finite-volume methods (quick search shows that there are some fixes for Riemann solvers), but I can't find almost any information regarding carbuncles in finite-difference methods.
Are there any known fixes for finite-difference methods? |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
I have no personal experience concerning the carbuncles problem. However, be careful on the fact that FD is a method based on the discretization of the differential form of the equations, a form that is not mathematically usable for simulating flows with discontinuities. For this reason you will find in literature the FV approach for such problems. |
||
|
|

|
||
|
|
|
#3 | |
|
Super Moderator
|
Quote:
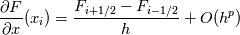 where 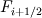 comes from a WENO scheme. comes from a WENO scheme.
|
||
|
|

|
||
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
Often a FV approach is denoted as a discretization of the divergence form of the equations while FD is denoted the discretization of the quasi-linear form. Actually, a real FV approach requires the definition of a volume for the integration of the divergence of the fluxes and is then defined by the flux reconstruction. For example, the book of Peric and Ferziger makes clear such distinction. While considering the discretization for hyperbolic systems, where the solution can become singular, the notation that adopts the divergence form has a special meaning. It works no longer on the pointwise functions but on the volume-averaged functions (as explained in the book of Leveque). For this reason a WENO reconstruction is suitable for solution with singularity. |
||
|
|

|
||
|
|
|
#5 |
|
Member
Oleg Sutyrin
Join Date: Feb 2016
Location: Russia
Posts: 41
Rep Power: 10  |
It seems that correct flux splitting is very important. I was using 3 versions (global and local Lax-Friedrich's and Roe-LLF) and was constructing flux splitting after weno-reconstruction of U and F(U) in local characteristic field. Now I weno-reconstruct already splitted flux. There are no more large-scaled carbuncles, but still are some weak shock front instabilities, so the question still stands.
Best results so far are obtained by proper Roe-LLF splitting with Roe averaging of Jacobians at x_j+1/2. |
|
|
|

|
|
|
|
|
#6 |
|
New Member
A, Smith
Join Date: Nov 2014
Posts: 4
Rep Power: 11  |
Here are a list of a few papers that address this problem. The "H"-correction can be applied to any of the flux splitting methods you've implemented.
Yu-Xin Ren, Maio’er Liu, and Hanxin Zhang. A characteristic-wise hybrid compact-WENO scheme for solving hyperbolic conservation laws. J. Comput. Phys., 192:365–386, 2003. doi:10.1016/j.jcp.2003.07.006. Richard Sanders, Eric Morano, and Marie-Claude Druguet. Multidimensional dissipation for upwind schemes: stability and applications to gas dynamics. J. Comput. Phys., 145(2):511–537, 1998. URL: http://www.sciencedirect.com/science...21999198960478, doi:http://dx.doi.org/10.1006/jcph.1998.6047. Maurizio Pandolfi and Domenic D’Ambrosio. Numerical instabilities in upwind methods: analysis and cures for the “Carbuncle” phenomenon. J. Comput. Phys., 166(2):271–301, 2001. doi:http://dx.doi.org/10.1006/jcph.2000.6652. |
|
|
|

|
|
|
|
|
#7 |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 14  |
So for all the paper that I went through uses additional or implicit numerical diffusion in the schemes to escape from carbuncles. I guess global Lax-Friedrich's scheme gives relatively less carbuncle than others u have considered. This is because it adds more numerical diffusion by using max(|u+c|) over the domain as characteristic speed. U can slightly increase this value. It will diffuse the result, especially at contact adding too much will end up in bad result. Almost all the contact capturing or less dissipative schemes give carbuncles. Another way is, u can add more artificial diffusion like Jameson's artificial viscosity after flux calculation before WENO interpolation.
|
|
|
|

|
|
|
|
|
#8 |
|
Member
Oleg Sutyrin
Join Date: Feb 2016
Location: Russia
Posts: 41
Rep Power: 10  |
After quick testing, H-correction seems to solve the problem! It removes both large-scale carbuncles and small-scale nearly-grid-aligned-shock instability.
The first 2 papers linked by Strat1994 are very useful for implementation. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| How to change the settings for FFD methods, please? | Xiaosong | SU2 | 3 | September 7, 2019 07:13 |
| Memory requirement for lattice boltzmann methods (simple BGK) | amaal | Hardware | 0 | January 18, 2011 12:14 |
| Velocity Under-relaxation in SIMPLE type methods | Matt U. | Main CFD Forum | 6 | July 4, 2005 06:29 |
| comments on FDM, FEM, FVM, SM, SEM, DSEM, BEM | kenn | Main CFD Forum | 2 | July 18, 2004 19:28 |
| SIMPLE, SIMPLER, Vorticity-Stream Methods Compared | Maciej Matyka | Main CFD Forum | 1 | June 17, 2003 06:48 |