 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Jul 2017
Posts: 6
Rep Power: 9  |
For incompressible NS equation in the finite volume discretization on a staggered grid, I have encountered a doubt.
We can put the diffusive term together with the advection term by factoring out gradient, for instance for x-direction for one term as below: 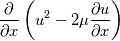 I am fine with the way to discretize the second term in staggered grid but for the first term in the code that I see someone has discretized the first term as 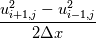 Why is this correct? Even if it is the central difference, shouldn't it also include 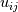 ? ?
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
The finite difference discretization below ensures proper conservation.
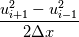 The advection term of the form 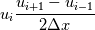 is not conservative and can lead to the numerical solution undershooting. As a side note, central differencing like that of the advection term can lead spurious oscillations. QUICK scheme or a stable advection scheme (ENO, WENO) can remedy such a problem. |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Join Date: Jul 2017
Posts: 6
Rep Power: 9  |
So you mean all is good with the conservative form of discretization? And no oscillations occur?
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Yes, you will want your scheme to be conservative. In terms of your second question, spurious oscillations can occur regardless if your scheme is conservative or not. A simple 1D example would be looking at the convection-diffusion equation and adjust the peclet number. You will find that upwind differencing will perform better than central differencing.
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
I agree, consider the Burgers equation in divergence and non-divergence (quasi-linear) form:
du/dt + d(u^2/2)/dx=d(mu*du/dx)/dx (divergence form) du/dt + u*du/dx=mu*d2u/dx^2 (quasi linear) No difference exists for the staggered or non staggered grid since the only involved variable is u. Discretize with second order central difference a see what happens. The appearence of u(i,j) in the convective term: d(u^2/2)/dx -> (u(i+1/2)^2-u(i-1/2)^2)/2/h du/dx -> (u(i+1/2)-u(i-1/2))/h Now you have two chance: 1) linear interpolation for u on the half-nodes 2) linear interpolation for u^2 on the half nodes The first choice is congruent to a linear reconstruction of the flux function, the second one introduces aliasing in the terms. |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
numerical oscillations are due to the lack of monotonicity of the scheme... Godunov theores states that monotonic linear scheme can be only first order accurate. Have also a look to the examples in the book of Peric & Ferziger
|
|
|
|

|
|
 |
| Tags |
| discretization scheme, navier stokes |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Why numerical diffusion is related to the advection term | Houthuys | Main CFD Forum | 6 | January 28, 2017 23:01 |
| Moving mesh | Niklas Wikstrom (Wikstrom) | OpenFOAM Running, Solving & CFD | 122 | June 15, 2014 07:20 |
| FVM discretization of diffusion term on crvlnr gr | Michail | Main CFD Forum | 3 | March 14, 2008 07:52 |
| Discretization of the Diffusion Term | Rui | CFX | 0 | October 24, 2005 13:43 |